12 KiB
网格噪声(Cellular Noise)
1996 年,在原始的 Perlin Noise 发布六年后,Perlin 的 Simplex Noise 发布五年前,Steven Worley 写了一篇名为“A Cellular Texture Basis Function”的论文。在这篇论文里,他描述了一种现在被广泛使用的程序化纹理技术。
要理解它背后的原理,我们需要从迭代开始思考。你可能已经知道迭代是什么意思:对,就是使用 for 循环。GLSL 的 for 循环中,只有一个需要注意的:我们检查循环是否继续的次数必须是一个常数(const). 所以,没有动态循环——迭代的次数必须是固定的。
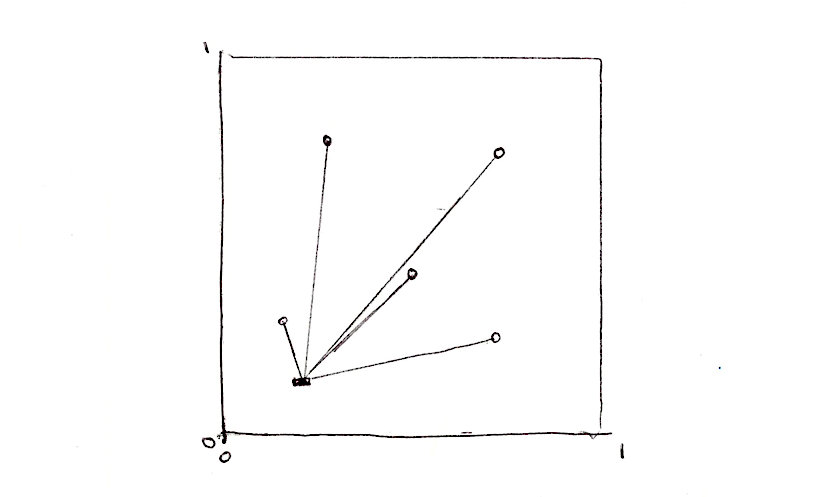
网格噪声基于距离场,这里的距离是指到一个特征点集最近的点的距离。比如说我们要写一个 4 个特征点的距离场,我们应该做什么呢?对每一个像素,计算它到最近的特征点的距离。也就是说,我们需要遍历所有 4 个特征点,计算他们到当前像素点的距离,并把最近的那个距离存下来。
float min_dist = 100.; // A variable to store the closest distance to a point
min_dist = min(min_dist, distance(st, point_a));
min_dist = min(min_dist, distance(st, point_b));
min_dist = min(min_dist, distance(st, point_c));
min_dist = min(min_dist, distance(st, point_d));
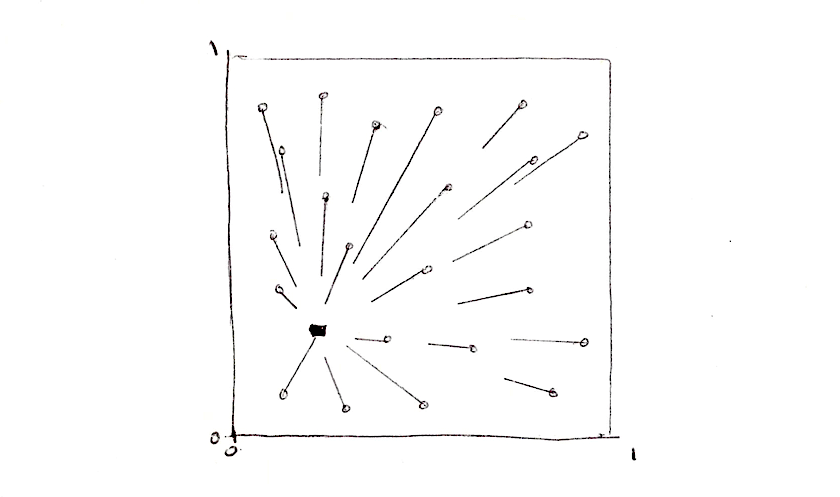
这种做法不是很优雅,但至少行得通。现在让我们用数组和 for 循环重写。
float m_dist = 100.; // minimum distance
for (int i = 0; i < TOTAL_POINTS; i++) {
float dist = distance(st, points[i]);
m_dist = min(m_dist, dist);
}
注意看我们用一个 for 循环遍历特征点集的数组,用一个 min() 函数来获得最小距离。下面是以上想法的简要的实现:
上面的代码中,其中一个特征点分配给了鼠标位置。把鼠标放上去玩一玩,你可以更直观地了解上面的代码是如何运行的。然后试试:
- 你可以让其余的几个特征点也动起来吗?
- 在读完关于形状的章节后,想象一些关于距离场的有意思的用法。
- 如果你要往距离场里添加更多的特征点怎么办?如果我们想动态地添加减少特征点数怎么办?
平铺和迭代
你可能注意到 GLSL 对 for 循环和 数组 似乎不太友好。如前所说,循环不接受动态的迭代次数。还有,遍历很多实例会显著地降低着色器的性能。这意味着我们不能把这个方法用在很大的特征点集上。我们需要寻找另一个策略,一个能利用 GPU 并行架构优势的策略。
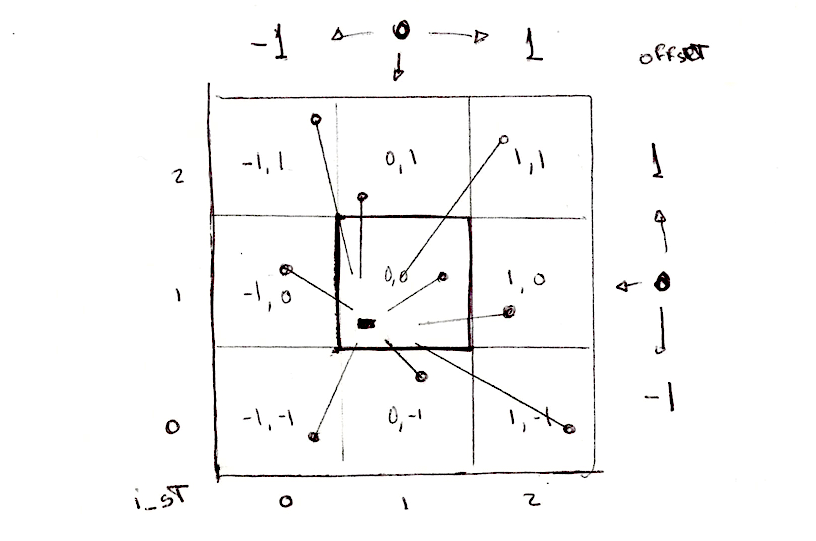
解决这个问题的一个方法是把空间分割成网格。并不需要计算每一个像素点到每一个特征点的距离,对吧?已经知道每个像素点是在自己的线程中运行,我们可以把空间分割成网格(cells),每个网格对应一个特征点。另外,为避免网格交界区域的偏差,我们需要计算像素点到相邻网格中的特征点的距离。这就是 Steven Worley 的论文中的主要思想。最后,每个像素点只需要计算到九个特征点的距离:他所在的网格的特征点和相邻的八个网格的特征点。我们已经在图案,随机和噪声这些章节介绍了如何把空间分割成网格,希望你已经熟悉这项技术。
// Scale
st *= 3.;
// Tile the space
vec2 i_st = floor(st);
vec2 f_st = fract(st);
那么,计划是什么呢?我们将使用网格坐标(存储在整数坐标 i_st 中)来构造特征点的随机位置。random2f 函数接受一个 vec2 类型参数,返回给我们一个 vec2 类型的随机位置。所以,在每个网格内,我们有一个特征点在随机位置上。
vec2 point = random2(i_st);
网格内的每个像素点(存储在浮点坐标 f_st 中)都会计算它到那个随机点的距离。
vec2 diff = point - f_st;
float dist = length(diff);
结果看起来就像这样:
我们还需要计算像素点到相邻网格中随机点的距离,而不只是当前的网格。我们需要 遍历 所有相邻网格。不是所有网格,仅仅是那些和当前网格相邻的网格。从网格坐标来说,就是 x 坐标从 -1 (左)到 1 (右), y 坐标从 -1 (下)到 1 (上)。一个 9 个网格的 3x3 区域可以用两个 for 循环遍历:
for (int y= -1; y <= 1; y++) {
for (int x= -1; x <= 1; x++) {
// Neighbor place in the grid
vec2 neighbor = vec2(float(x),float(y));
...
}
}
现在,我们可以在双 for 循环中计算相邻网格中随机点的位置,只需要加上相邻网格对当前网格的偏移量。
...
// Random position from current + neighbor place in the grid
vec2 point = random2(i_st + neighbor);
...
剩下的部分就是计算像素点到那个随机点的距离,并把最近的距离存到变量 m_dist(minimum distance)里面.
...
vec2 diff = neighbor + point - f_st;
// Distance to the point
float dist = length(diff);
// Keep the closer distance
m_dist = min(m_dist, dist);
...
上面的代码源自这篇 Inigo's Quilez 的文章,他写道:
“可能值得注意的是,上面的代码中有一个很漂亮的技巧。多数实现都存在精度问题,因为他们是在“域”空间(如“世界”或“对象”空间)内产生随机点,这可能是里原点任意远的。要解决这个问题,可以使用更高精度的数据类型,或更聪明些。我的实现不是在“域”空间(如“世界”或“对象”空间)内产生随机点,而是在“网格”空间内:一旦提取了着色点的整数和小数部分,我们当前的网格就确定了,我们所关心的就是这个网格周围发生了什么,意味着我们可以将所有坐标的整数部分放在一起,从而节省了许多精度位。事实上,一个常规的 voronoi 实现中,从着色点减去随机特征点时,点坐标的整数部分简单地消除掉了。上面的实现中,我们甚至不会让这种消除发生,因为我们正在把所有的计算移到“网格”空间。这个技巧可以让你处理这种情况: 你想要把 voronoi 用在整个星球上——可以简单地将输入替换为双精度,执行 floor() 和 fract() 计算,其余的计算仍使用浮点数,省去了将整个实现改成双精度的成本。当然,同样的技巧也适用于 Perlin Noise 模式(但是我还没有在任何地方看到过它的实现或记录)。”
简要重述一遍:我们把空间分割成网格,计算每个像素点到它所在网格中的那个特征点的距离,和它到相邻的八个网格中的特征点的距离,结果是一个距离场,如下所示:
进一步探索:
- 缩放空间。
- 你有其它办法让那些特征点动起来吗?
- 如果我们想要加入一个鼠标位置作为其中一个特征点怎么办?
- 有没有其它办法构造这个距离场,除了
m_dist = min(m_dist, dist);之外? - 用这个距离场你可以创造出什么有意思的图案?
这个算法也可以从特征点而非像素点的角度理解。在那种情况下,算法可以表述为:每个特征点向外扩张生长,直到它碰到其它扩张的区域。这反映了自然界的生长规则。生命的形态是由内部扩张、生长的力量和限制性的外部力量共同决定的。模拟这种行为的算法以 Georgy Voronoi 命名。
Voronoi 算法
用网格噪声构造 Voronoi 图远没有看上去的那么难。我们只需要保留一些关于最近的特征点的额外信息。我们将要用到一个叫 m_point 的 vec2 类型变量存储像素点到最近的特征点的向量,而不只是距离。
...
if( dist < m_dist ) {
m_dist = dist;
m_point = point;
}
...
注意在下面的代码中,我们不再使用 min 来计算最近距离,而是用一个普通的 if 语句。为什么?因为当一个新的更近的特征点出现的时候,我们还需要保存它的位置(32 行至 37行)。
注意那个移动的(鼠标位置下面那个)细胞的颜色是如何根据它的位置而改变的。那是因为它的颜色由最近特征点决定。
就像我们之前所做的那样,现在是扩大规模的时候,转而使用 Steven Worley 的论文中的方法。试着自己实现它。你可以通过点击下面的示例来获取帮助。注意 Steven Worley 的原始方法中,每个网格的特征点数是可变的,对大多数网格来说不止一个。在他的 C 语言实现中,这是用来提早退出来加速循环。GLSL 循环不允许动态的迭代次数,所以你可能更希望一个网格对应一个特征点。
一旦你弄清楚了这个算法,想想它有什么有趣、有创意的用途。
优化 Voronoi
在 2011 年, Stefan Gustavson 优化了 Steven Worley 的算法,仅仅对一个 2x2 的矩阵作遍历(而不是 3x3 的矩阵)。这显著地减少了工作量,但是会在网格边缘制造人工痕迹。看看下面的例子。
Later in 2012 Inigo Quilez wrote an article on how to make precise Voronoi borders.
Inigo 在 Voronoi 上的实验并没有就此停止。2014 年,他写了一篇非常漂亮的文章,提出一种他称作为 voro-noise 的噪声,可以让常规噪声和 voronoi 逐渐地融合。用他的话说:
“尽管有这样的相似之处,但事实上,两种模式中网格的使用方式都是不同的。噪声会内插或平均随机值(如值噪声),而 Voronoi 是计算到最近特征点的距离。平滑双线性插值和最小值评估是两个非常不同的操作,或者……它们是否能用更广义的方法组合?如果是这样,那么噪声和 Voronoi 模式都可以被看作是一种更一般的以网格为基础的模式生成器?”
现在,是时候仔细观察事物,去接受自然的启发,并用这项技术发现你自己的风景!