mirror of https://github.com/patriciogonzalezvivo/thebookofshaders synced 2024-11-11 13:10:57 +00:00

lukas 9d5c80fd11 updating flong links

2020-11-27 01:23:53 -05:00

12 KiB

Raw Blame History

Disegno Algoritmico

Funzioni di forma

Questo capitolo potrebbe essere chiamato "la lezione del recinto di Mr. Miyagi". In precedenza abbiamo associato la posizione normalizzata di x e y ai canali rosso e verde. Fondamentalmente abbiamo creato una funzione che prende un vettore bidimensionale (x e y) e restituisce un vettore quadridimensionale (r, g, b e a). Ma prima di andare avanti nella trasformazione dei dati tra dimensioni, dobbiamo iniziare da qualcosa di più semplice…molto più semplice. Questo significa comprendere come creare funzioni unidimensionali. Maggiori sono l’energia e il tempo che impieghi nel comprendere e nel padroneggiarle, migliore sarà il tuo karate shader.

La seguente struttura di codice sarà la nostra recinzione. In questa visualizziamo il valore normalizzato della coordinata x (st.x) in due modi: uno con la luminosità (osserva il bel gradiente dal nero al bianco) e l’altro tracciando sopra una linea verde (in questo caso il valore di x è assegnato direttamente al valore di y). Non ti concentrare troppo sulla funzione plot, la vedremo nel dettaglio tra poco.

Nota veloce: il costruttore di tipo vec3 "capisce" che vuoi assegnare i tre canali di colori allo stesso valore, mentre vec4 capisce che vuoi costruire un vettore a quattro dimensioni con tre unidimensionali più un quarto valore (in questo caso il valore che controlla l’alfa o l’opacità). Guarda, ad esempio, le righe 19 e 25 qui sopra.

Questo codice è il tuo recinto; è importante osservarlo e capirlo. Tornerai spesso in questo spazio tra 0.0 e 1.0. Imparerai l’arte di combinare e modellare questa linea.

Questa relazione uno a uno tra x e y (o la luminosità) è conosciuta come interpolazione lineare. A partire da qui, possiamo usare alcune funzioni matematiche per modellare la linea. Per esempio, possiamo elevare x alla quinta potenza e creare una linea curva.

Interessante, vero? Alla riga 22 prova esponenti diversi, per esempio: 20.0, 2.0, 1.0, 0.0, 0.2 e 0.02. comprendere questa relazione tra il valore e l’esponente sarà molto utile. Questo genere di funzioni matematiche ci darà un controllo espressivo sul codice, come una specie di agopuntura che permette di controllare il flusso dei valori.

pow() è una funzione nativa il GLSL e ce ne sono molte altre. La maggior parte di queste sono accelerate al livello dell’hardware; ciò significa che se esse sono usate in modo appropriato e con discrezione, renderanno il tuo codice molto più veloce.

Sostituisci la funzione alla riga 22. Provane altre, come: exp(), log() e sqrt(). Alcune di queste funzioni sono più interessanti quando le si utilizza con PI. Puoi vedere alla riga 8, che ho definito un macro che sostituisce qualsiasi chiamata a PI con valore 3.14159265359.

Step e Smoothstep

GLSL ha anche alcune funzioni interpolanti native uniche che sono accelerate dall’hardware.

L’interpolazione step() riceve due parametri. Il primo è il limite o la soglia, mentre il secondo è il valore che volgiamo controllare. Qualsiasi valore al di sotto del limite tornerà a 0.0, mentre tutto ciò al di sopra del limite tornerà a 1.0.

Prova a cambiare il valore della soglia alla riga 20 del seguente codice.

L’altra funzione unica è conosciuta come smoothstep(). Data una serie di due numeri e un valore, questa funzione interpolerà il valore tra la serie definita. I primi due parametri sono per l’inizio e la fine della transizione, mentre il terzo è per il valore d’interpolazione.

Nell’esempio precedente, alla riga 12, nota che abbiamo usato smoothstep ( ) per disegnare la linea verde sulla funzione plot(). Per ciascuna posizione lungo l’asse x, questa funzione crea un salto ad un particolare valore di y. Come? Collegando tra di loro due smoothstep(). Guarda la funzione qui di seguito, sostituiscila alla riga 20 di sopra e pensa ad esso come ad un taglio verticale. Lo sfondo assomiglia ad una linea, vero?

    float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Seno e coseno.

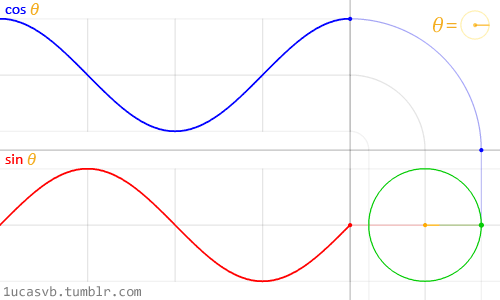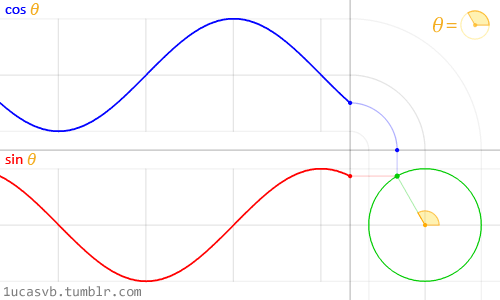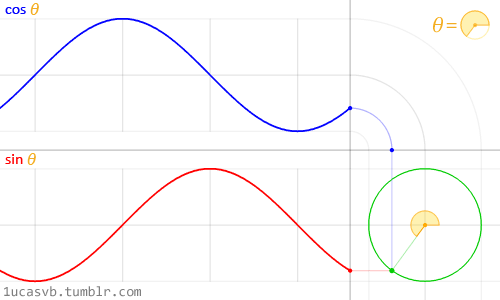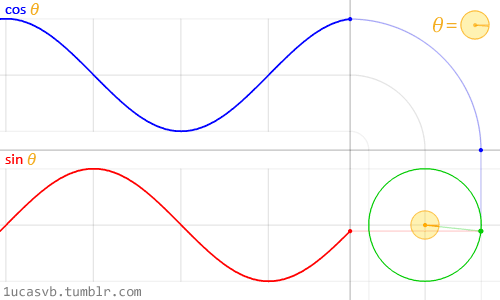
Quando si vuole usare la matematica per animare, modellare o combinare, non c’è nulla di meglio che essere amici del seno e del coseno.

Queste due basiche funzioni trigonometriche lavorano congiuntamente per costruire cerchi che sono utili come il coltellino svizzero di MacGyver. È importante sapere come si comportano e in che modo possono essere combinate. In breve: dato un angolo (in radianti), essi ritorneranno alla corretta posizione di x (cosine) e di y (sine) di un punto sul margine del cerchio con raggio uguale a 1. Il fatto che queste funzioni ritornano ai valori normalizzati ( tra -1 e 1) in modo così armonioso e fluido le rende uno strumento incredibile.

Mentre è difficile descrivere tutte le relazioni tra le funzioni trigonometriche e i cerchi, le animazioni soprastanti le riassumono molto bene visivamente.

Guarda attentamente questa curva sinusoidale. Nota come i valori di y ondeggiano dolcemente tra +1 e -1. Come abbiamo visto nell’esempio del tempo nel capitolo precedente, si può usare questo comportamento ritmico di sin() per animare le proprietà. Se stai leggendo questo esempio su un browser, vedrai che puoi cambiare il codice nella formula soprastante per osservare come cambia l’onda. (Nota: non dimenticare il punto e virgola alla fine delle righe).

Prova questi esercizi e osserva cosa succede:

Aggiungi tempo (u_time) a x prima di calcolare sin. Osserva attentamente questo movimento lungo x.
Moltiplica x per PI prima di calcolare sin. Nota come le due fasi si restringano e ciascun ciclo si ripeta tra due valori interi.
Moltiplica tempo (u_time) per x prima di calcolare sin. Osserva come la frequenza tra le fasi diventi sempre più compressa. Nota che u_time può avere già assunto un valore molto grande, rendendo il grafico difficile da leggere.
Aggiungi 1.0 a sin(x). Osserva come tutte le onde siano dislocate verso l’alto e adesso tutti i valori siano tra 0.0 e 2.0.
Moltiplica sin(x) per 2.0. Osserva come l’ampiezza raddoppi di misura.
Calcola il valore assoluto (abs()) di sin(x). Sembra la traccia di una palla che rimbalza.
Estrai solo la parte frazionaria (fract()) della risultante di sin(x).
Aggiungi il numero intero più elevato (ceil()) e il più basso (floor()) della risultante di sin(x) per ottenere un’onda digitale dei valori 1 e -1.

Altre funzioni utili

AAl termine dell’ultimo esercizio abbiamo presentato alcune nuove funzioni. È arrivato il momento di provare con ciascuna, decommentando le righe sottostanti, una alla volta. Impara quete funzioni e studia il loro comportamento. Lo so, ti stai chiedendo perché e se cerchi velocemente su Google "arte generativa" capirai subito. Ricorda che queste funzioni sono il nostro recinto. Stiamo controllando il movimento in una dimensione, su e giù. Presto arriverà il momento per due, tre e quattro dimensioni!

Funzioni di forma avanzate

Golan Levin possiede un’ampia documentazione molto utile sulle funzioni di forma complesse. Trasportare queste funzioni in GLSL è un ottimo modo per incominciare a costruire la propria cassetta degli attrezzi per creare codici.

Come i cuochi collezionano con passione spezie e ingredienti esotici, così gli artisti digitali e i creative coders adorano lavorare sulle proprie funzioni di forma.

Iñigo Quiles possiede una grande raccolta di funzioni molto utili. Dopo aver letto quest'articolo, leggi le seguenti traduzioni di queste funzioni in GLSL. Fai attenzione ai piccoli cambiamenti necessari, come mettere "."" (punto) sui valori flessibili, e usare il nome GLSL per le funzioni in C; per esempio, invece di powf(), usa pow():

Per mantenere alta la tua motivazione, qui trovi un esempio elegante dell’essere esperti nel karate delle funzioni di forma (creato da Danguafer).

Nel Prossimo >> capitolo inizieremo ad usare nuove mosse. Prima mescolando i colori e poi disegnando forme.

Esercizio

Guarda la seguente tabella di equazioni fatta da Kynd. Osserva come combini le funzioni e le loro proprietà per controllare i valori tra 0.0 e 1.0. Ora è il tuo momento di fare pratica replicando queste funzioni. Ricordati: più ti eserciti, migliore sarà il tuo karate.

Per la tua cassetta degli attrezzi

Qui trovi alcuni strumenti che ti faciliteranno la visualizzazione di questi tipi di funzione.

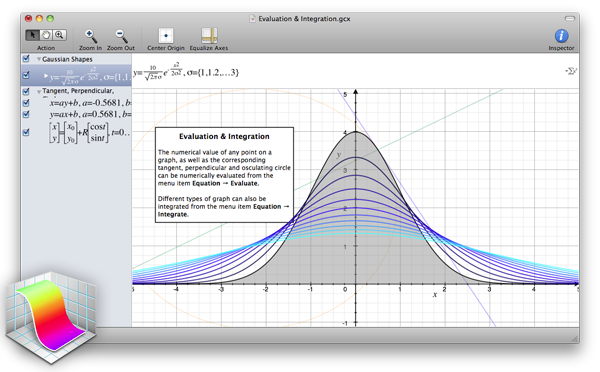
Grapher: se hai un computer MacOS, digita grapher nel tuo spotlight e riuscirai ad usare questo magnifico attrezzo.

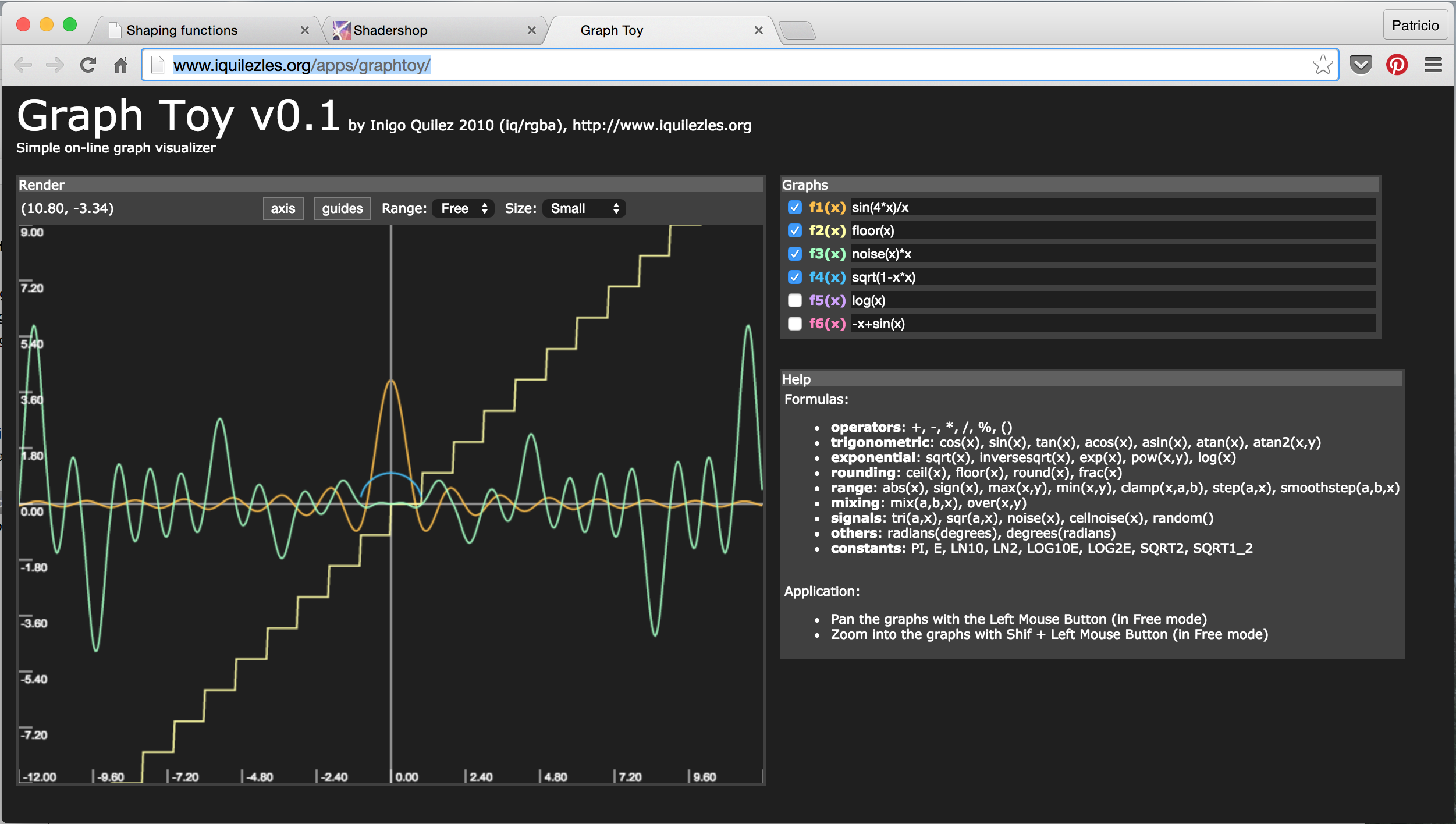
GraphToy: ancora una volta Iñigo Quilez ha creato un mezzo per visualizzare le funzioni GLSL in WebGL.

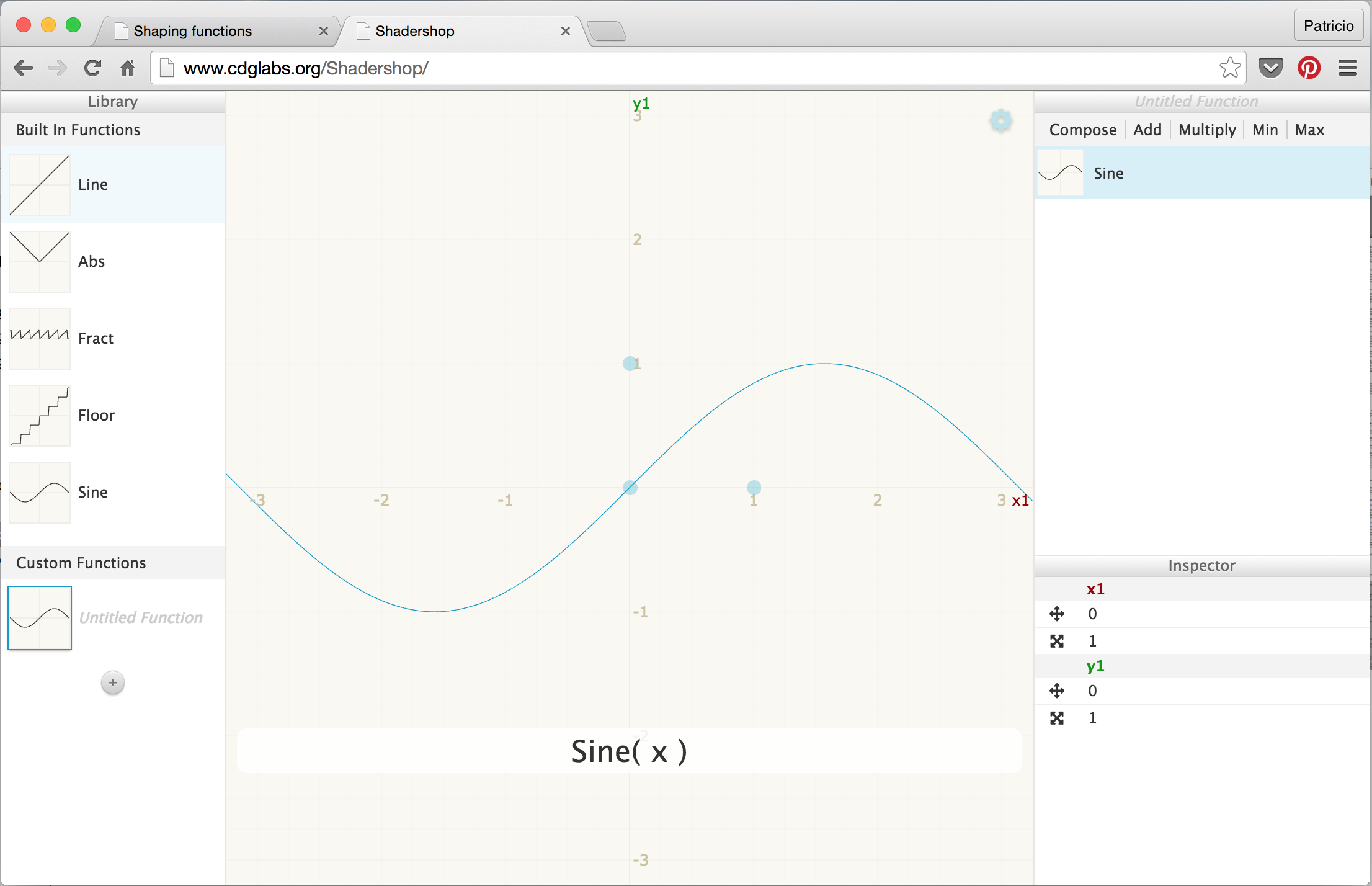
Shadershop: questo favoloso mezzo creato da Toby Schachman ti insegnerà a costruire funzioni complesse in un modo visivo ed incredibilmente intuitivo.

12 KiB Raw Blame History Unescape Escape