14 KiB
رسم الگوریتمی
توابع شکلی
این قسمت از آموزش را میتوان درس حصار آقای میاگی نامگذاری کرد. در قسمت قبل ما موقعیت نرمالایز شده x و y را به کانال قرمز و سبز مپ کردیم. اساسا ما تابعی ایجاد کردیم که دو بردار x و y میگیرد و یک بردار چهار بعدی r,g,b,a بر میگرداند. اما قبل از اینکه به تبدیل داده ها بین بعد ها بپردازیم، باید از خیلی ساده تر شروع کنیم...خیلی ساده تر. یعنی چگونگی ساخت تابع یک بعدی. هرچه زمان و انرژی بیشتری برای تسلط و یادگیری آن صرف کنید، قدرت شیدر نویسی شما بهتر میشود.
ساختار کد زیر حصار ما خواهد بود. در آن ما مقدار نرمالایز شده x را (st.x) به دو روش نمایش میدهیم. یکی با روشنایی (گرادیان سیاه به سفید) و دیگری با ترسیم خط سبز (مقدار x برابر y). خیلی روی تابع plot تمرکز نکنید. بزودی در مورد آن بیشتر میفهمید.
نکته: کانستراکتور vect3 در مثال بالا میفهمد میخواهید 3 کانال آن را با یک مقدار پر کنید، همچنین vect4 میفهمد میخواهید یک بردار 4 بعدی با استفاده از یک بردار سه بعدی و یک ورودی دیگر بسازید. در این مورد عدد چهارم آلفا هست.
این کد حصار شماست. مهم است که آن را مشاهده و درک کنید.، شما بارها و بار ها به این فضا باز خواهید گشت. شما استاد ترکیب و نقش دادن این شکل میشوید.
این رابطه یک به یک بین x, y یا همین روشنایی به عنوان درون یابی خطی (linear interpolation) شناخته میشود. در این مثال میتوان با کمی ریاضیات به خط شکل بدهیم. برای مثال میتوان x را به توان 5 رساند و یک خط منحنی تشکیل داد.
جالب است، اینطور نیست؟ در خط 22 عدد های مختلف را امتحان کنید مثل : 20.0 ,0.02, 2.0, 1.0, 0.0, 0.2 . درک رابطه بین مقدار و توان بسیار مفید خواهد بود. استفاده از این نوع توابع ریاضی در جاهای متخلف به شما امکان کنترل جریان مقادیر را امکان میسازد.
توان() یکی از تابع های تعبیه شده در GLSL هست. بیشتر این توابع در سطح سخت افزار شتابدهی میشوند. به این معنا که اگر درست استفاده شوند، کد شما را سریع میکنند.
عملکرد توان در خط 22 را با عملکرد های مقابل جایگزین کنید: exp(), log(), sqrt(). بعضی از این توابع را اگر با عدد پی ترکیب کنید بسیار جالب میشوند. در خط 8 میبینید که بجای استفاده از خود عدد PI،
من یک ماکرو تعریف کرده ام.
Step و Smoothstep
GLSL همچنین دارای چندین تابع خاص تعبیه شده است که توسط سخت افزار شتاب دهی میشوند.
step() دو پارامتر دریافت میکند. اولی حد یا همان آستانه است و دومی مقداریست که میخواهیم بررسی کنیم یا عبور دهیم. اگر مقدار ورودی در این حد باشید، مقدار 0 را بر میگرداند، در حالی که بقیه مقادیر بالای حد مجاز مقدار 1 را بر میگردانند.
مقدار حد را در خط 20 سعی کنید تغییر دهید و نتیجه را مشاهده کنید.
تابع دیگر در این مورد smoothstep() یک دامنه دو عددی را دریافت و ورودی سوم را با آن ها مقایسه میکند. اگر وردی بین آن دو عدد بود مقدار پخش شده بین 0 و 1 برگردانده میشود ولی اگر مقدار ورودی سوم کوچکتر یا بزرگتر از بازه بود مقادیر 0 یا 1 برگردانده میشود.
در خط 12 مثال قبل ما از smoothstep برای کشیدن خط سبز در تابع 'plot' استفاده کردیم. برای هر مقدار x تابع ما یک مقدار خاص y تولید میکند اما چگونه؟ با اتصال دو smoothstep به هم. به تابع زیر نگاه کنید، در خط 20 کد را جایگزین کنید، پس زمینه شبیه یک خط شد؟
float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);
Sine and Cosine
اگر میخواهید برای انیمیت، شکل دهی، یا ترکیب مقادیر از ریاضیات استفاده کنید، هیچ چیز بهتر از دوست شدن با سینوس و کسینوس نیست.
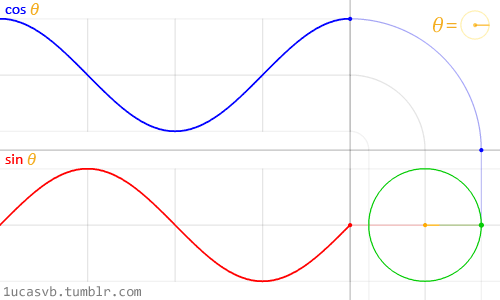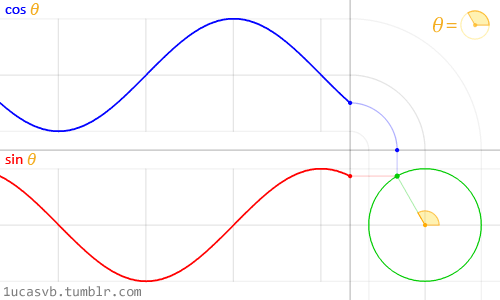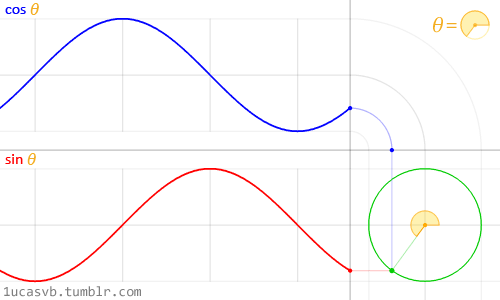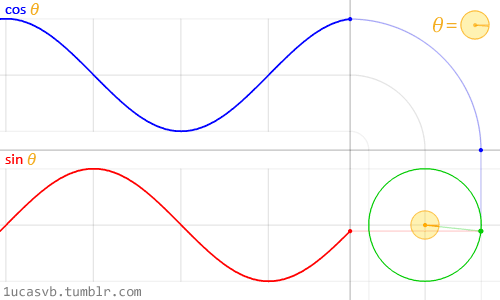
این دو عملکرد اساسی مثلثاتی با هم کار میکنند تا دایره هایی را بسازند که به اندازه چاقوی ارتش سوئیس مفید باشند. بسیار مهم است که بدانید چگونه رفتار میکنند و چگونه میتوان آنان را ترکیب کرد. به طور خلاصه، آنان با توجه به زاویه، موقعیت (cosine) یا همان x و (sine) یا همان y یک نقطه را در لبه دایره با شعاع 1 بر میگردانند. این واقعیت که آنان مقادیر نرمالایز شده بین -1 و 1 به طور نرم برمیگردانند، آنان را به ابزاری باور نکردنی تبدیل میکند.
اگرچه توصیف تمام روابط مثلثاتی و دایره ها دشوار است اما انیمیشن فوق خلاصه ای از این روابط را به شما نمایش میدهد.
نگاهی دقیق به این موج سینوسی بیاندازید که چگونه مقادیر y به طور نرم و پیوسته بین -1 و 1 در جریان است. همانطور که در مثال های قسمت قبل دیدیم شما میتوانید از این رفتار سینوسی برای انیمیت مقادیر استفاده کنید. اگر این مثال را روی مرورگر میخوانید پس میتوانید کد فرمول بالا را تغییر دهید و نحوه تغییر موج را مشاهده کنید. توجه: نقطه ویرگول را در آخر سطر ها فراموش نکنید.
این تمرین ها را انجام دهید و نتیجه را ببینید:
-
قبل از محاسبه سینوس به x مقدار u_time را اضافه کنید. در امتداد x حرکت خواهد کرد.
-
قبل از محسبه سینوس x را در عدد PI ضرب کنید. میبینید که چگونه .نمودار جمع میشود و در هر دو مقدار صحیح یک چرخه اتفاق میافتد
-
اینبار u_time را قبل از محاسبه سینوس در x ضرب کنید، مشاهده میکنید که فرکانس بیشتر و بیشتر فشرده میشود، توجه کنید شاید u_time عدد خیلی بزرگی باشد و نتوانید نموادار را مشاده کنید. در این صورت صفحه را دوباره بارگذاری کنید.
-
1.0 را به سینوس x اضافه کنید. تمام نمودار یک واحد بالا میرود و مقادیر بین 0 و 2 نوسان میکنند.
-
سینوس x را در 2.0 ضرب کنی، و تغییرات را ببینید
-
مقدار قدر مطلق (
abs()) سینوس را سعی کنید مشاهده کنید، مانند اثرات جهش توپ خواهد شد. -
قسمتی کسری (
fract()) سینوس X را مشاهده کنید. -
بزرگترین عدد صحیح (
ceil()) و کوچکترین عدد صحیح (floor()) را به نتیجهsin(x)اعمال کنید، تا یک موج دیجیتال از مقادیر 1 و -1 ببینید.
برخی توابع مفید دیگر
در این انتها توابع جدیدی را معرفی کرده ایم. اکنون زمان آن است که یکی یکی آنان را امتحان کنید. این عملکرد ها را بشناسید و نحوه رفتار آنان را مطالعه کنید، شاید تعجب کرده این و میگویید چرا؟ یک جستجوی گوگل در مورد "generative art" شما را آگاه میکند. حواستان باشد این توابع حصار های ما هستند. ما در یک بعد در حال استاد شدن هستیم، بزودی نوبت به ابعاد دو و سه و چهار میشود.
توابع شکل دهی پیشرفته
Golan Levin دارای داکیومنت عالی از عملکرد های پیچیده تر شکل دهی است، که فوق العاده مفید هستند. برای ساخت منابع کد خودتان، انتقال آنان به GLSL حرکتی بسیار هوشمندانه است
-
توابه شکل دهنده چند جمله ای: www.flong.com/archive/texts/code/shapers_poly
-
توابه شکل دهنده نمایی: www.flong.com/archive/texts/code/shapers_exp
-
توابه شکل دهنده دایره ای و بیضوی: www.flong.com/archive/texts/code/shapers_circ
-
توابع Bezier و سایر پارامتر های شکل دهنده: www.flong.com/archive/texts/code/shapers_bez
مانند سرآشپز ها که ادویه و مواد مختلف و عجیب را جمع آوری میکنند، هنرمندان دیجیتال و برنامه نویسان خلاق هم، علاقه خاصی به استفاده از تابع های مخصوص به خود دارند.
Iñigo Quiles مجموعه ای عالی از توابع مفید دارد. بعد از خواندن این مقاله نگاهی به توابع ترجمه شده به GLSL آن بیاندازید. به تغییرات کوچکی که لازم هستند دقت کنید مانند نقطه در اعداد شناور و استفاده از نام GLSL برای توابع C، برای مثال بجای powf() از pow() استفاده شده.
برای بالا بردن انگیزه تان در اینجا یک مثال از (Danguafer) آوردم. که نشان دهنده توانایی بالا او در توابع شکل دهنده است.
در قسمت بعد چیز های جدیدی را یاد میگیریم، ابتدا مخلوط کردن نگ ها و سپس ترسیم اشکال را مرور خواهیم کرد.
تمرین
به جدول معادلات زیر که توسط Kynd ساخته شده است، نگاه بیاندازید. ببینید چگونه او توابع وخصوصیات آنان را برای کنترل مقادیر بین 0.0 تا 1.0 ترکیب میکند. حال نوبت شما است که این توابع را تکرار و تمرین کنید. به یاد داشته باشید هر چه بیشتر تمرین کنید کاراته شما بهتر خواهد شد.(اشاره به موضوع اول این بخش)
جعبه ابزار
در اینجا چند ابزار آورده شده که تجسم نوع عملکرد و توابع را برای شما آسان میکند.
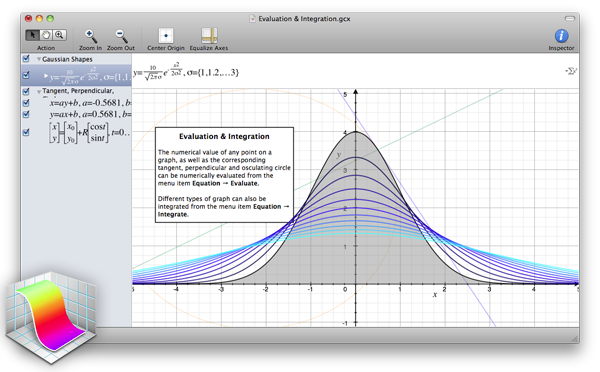
- Grapher: اگر یک سیستم مک دارید در اسپات لایت خود grapher را تایپ کنید تا ازین ابزار بسیار مفید استفاده کنید.
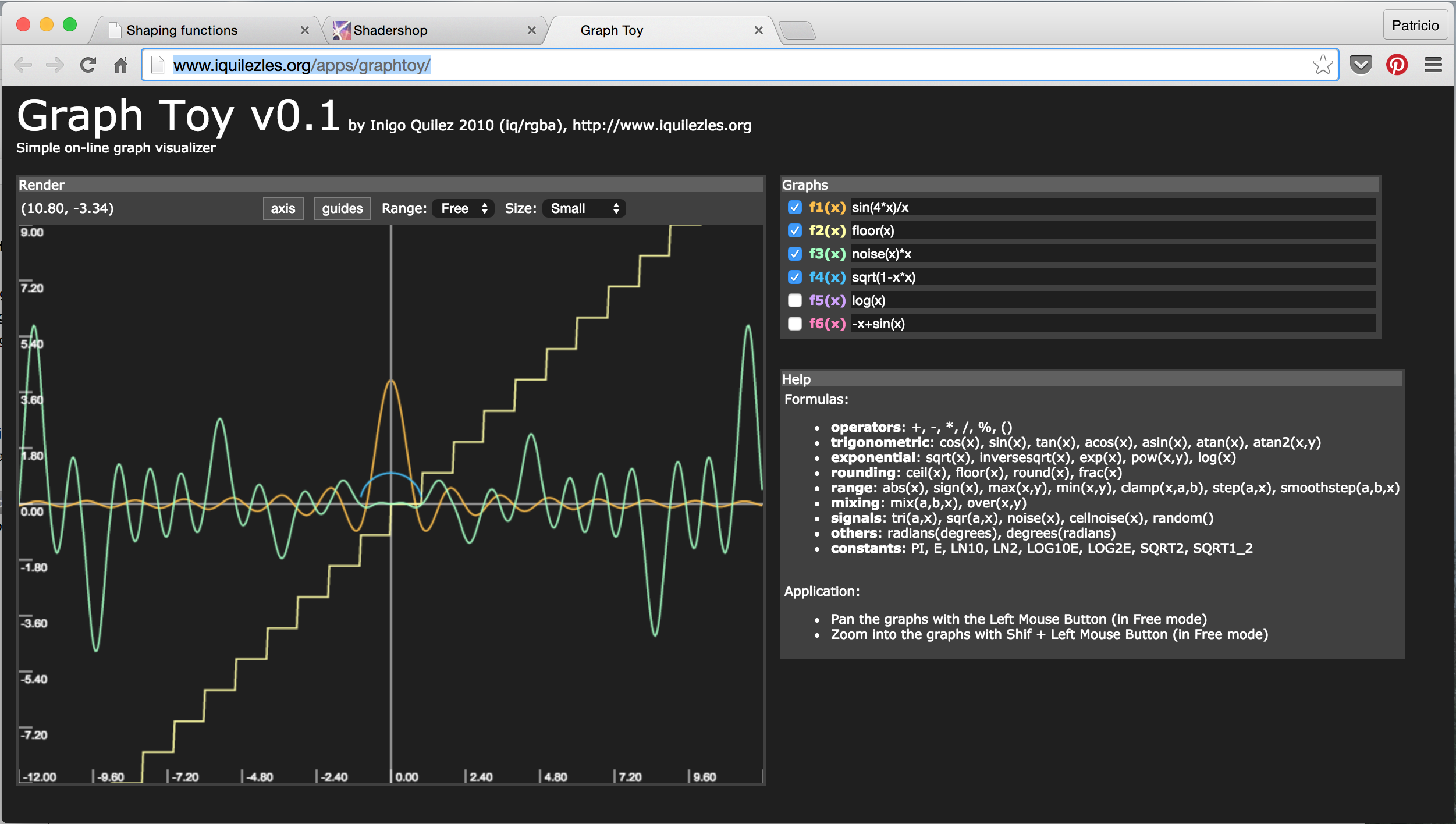
- GraphToy: دوباره Iñigo Quilez او ابزاری برای تجسم توابع GLSL در WEBGL ساخته است.
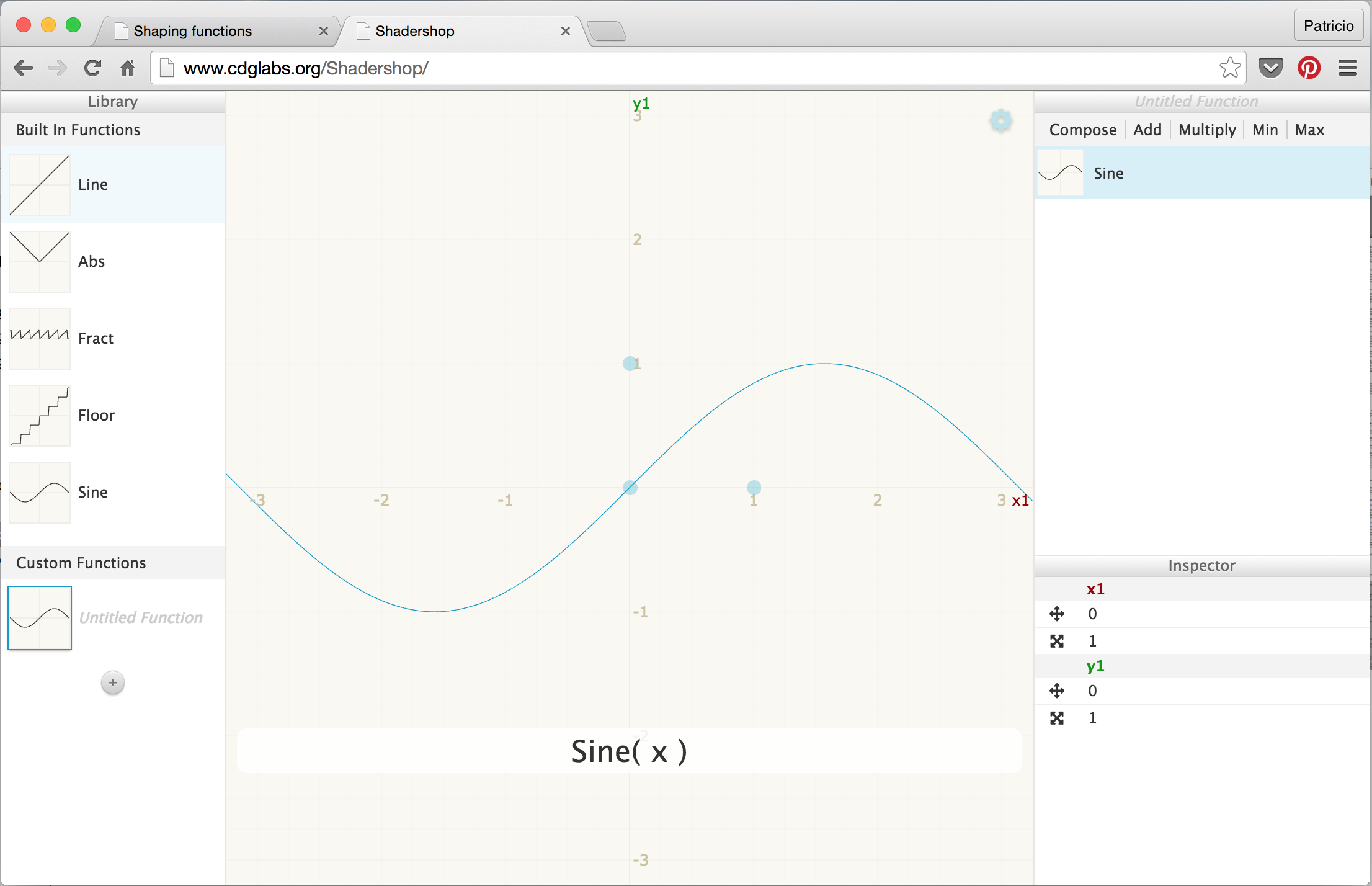
- Shadershop: این ابزار شگفت انگیز توسط Toby Schachman ساخته شده است که به شما می آموزد چگونه توابع پیچیده را به روش بصری به طور باورنکردنی بسازید.