thebookofshaders/07/README-fa.md

اشکال

بالاخره! برای این لحظه آماده شده ایم، شما بیشتر مبانی و توابع GLSL را آموخته اید. معادلات شکلی دهی را تمرین کرده اید، اکنون زمان جمع بندی است. شما برای این چالش آماده هستید! در این قسمت شما نحوه رسم اشکل ساده را بصورت موازی می‌آموزید.

مستطیل

تصور کنید کاغذی شبکه ای مانند آنچه در کلاس ریاضیات داشتیم در اختیار داریم، و تکلیف ما رسم مربع است، اندازه کاغذ 10x10 و مربع باید 8x8 باشد. شما چه کار خواهید کرد؟

شما به جز سطر های اول و اخر و ستون اول و آخر همه را رنگ می‌زنید، اینطور نیست؟

این مثال چه ربطی به شیدر ها دارد؟ هر مربع کوچک از کاغد شبکه مان مانند یک ترد(پیکسل) است. همچنین هر مربع کوچک مانند صفحات شطرنج مختصات خودر را می‌داند. در قسمت های قبلی ما رنگ های قرمز و سبز را به مقادیر x,y مپ کردیم، و یاد گرفتیم چگونه در مسائل دو بعدی از مقادیر بین 0.0 تا 1.0 استفاده کنیم، چگونه می‌توان از این موضوع برای ترسیم یک مربع در وسط صفحه کنوس استفاده کرد؟

بیایید با استفاده از دستورات شبه کد شروع کنیم، یعنی دستورات if را استفاده کنیم. اصول انجام این کار به طرز چشم گیری شبیه سناریوی کاغذ شبکه ای است.

if ( (X GREATER THAN 1) AND (Y GREATER THAN 1) )
    paint white
else
    paint black

حالا که می‌دانیم چگونه کار می‌کند بیاید بجای استفاده از دستور شرطی از step() استفاده کنیم, و همچنین بجای استفاده از 10*10 از مقادیر بین 0.0 و 1.0 استفاده کنیم.:

uniform vec2 u_resolution;

void main(){
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    vec3 color = vec3(0.0);

    // Each result will return 1.0 (white) or 0.0 (black).
    float left = step(0.1,st.x);   // Similar to ( X greater than 0.1 )
    float bottom = step(0.1,st.y); // Similar to ( Y greater than 0.1 )

    // The multiplication of left*bottom will be similar to the logical AND.
    color = vec3( left * bottom );

    gl_FragColor = vec4(color,1.0);
}

تابع step() پیکسل های زیر 0.1 را به سیاه تبدیل می‌کند (vec3(0.0)) و بقیه تبدیل به سفید می‌شوند (vec3(1.0)) . ضرب بین left و bottom مانند عمکرد and کار ‌می‌کند، جایی که هردو باید 1.0 باشند، 1.0 برمی‌گرداند. این عمل باعث کشیدن دو خط در پایین و سمت چپ کنوس میشود..

در کد قبلی ما ساختار را برای قسمت پایین و چپ تکرار کردیم. می‌توان با پاس دادن یک بردار دو بعدی یه step() چند خط در کد صرفه جویی کنیم. به این صورت :

vec2 borders = step(vec2(0.1),st);
float pct = borders.x * borders.y;

تا الان فقط دو حاشیه پاین و چپ مستطیل را رسم کرده ایم. بیایید دو مورد دیگر را هم انجام دهیم. کد زیر را بررسی کنید:

خطوط 21 و 22 را از کامنت خارج کنید و دقت کنید که چگونه مختصات St را معکوس کردیم و عملکرد Step را بصورت مشابه روی آن اعمال شد. در این حالت vec2(0.0,0.0) بالا سمت راست کنوس خواهد بود. این یک مثال دیجیتالی از برگرداندن ورق کاغذ و استفاده مجدد عملیات است..

توجه کنید در خط 18 و22 تمام طرفین در هم ضرب می‌شوند که معادل نوشتن عبارت زیر است:

vec2 bl = step(vec2(0.1),st);       // bottom-left
vec2 tr = step(vec2(0.1),1.0-st);   // top-right
color = vec3(bl.x * bl.y * tr.x * tr.y);

جالب بود؟ این تکنک تماما در مورد استفاده ازstep() و ضرب و برگرداندن مختصات است.

قبل از ادمه دادن سعی کنید تمرینات زیر را انجام دهید:

• اندازه و نسبت مستطیل را تغییر دهید.

• با استفاده از همین کد از smoothstep() بجای step() استفاده کنید. توجه کنید با تغییر مقادیر می‌توانید از لبه های بلوری به حاشیه های صاف و ظریف بروید.

• عملیات دیگری انجام دهید که از floor() استفاده کند.

• یک شکل مورد علاقه خود را پیاده سازی کنید، و تابعی در آن ایجاد کنید که در آینده هم بتوانید از آن استفاده مجدد کنید، عملکرد خود را انعطاف پذیر و کارامد کنید.

• ِیک تابع دیگر بسازید که فقط اضلاع مستطیل را نمایش دهد.

• فکر می‌کنید چگونه می‌توان مستطیل های بیشتری در بیلبورد قرار داد و آن ها را متحرک ساخت? اگر راهش را پیدا کردید ترکیبی از مستطیل ها و رنگ های مختلف شبیه نقاشی Piet Mondrian بکشید.

دایره ها

ترسیم مربع و مستطیل روی کاغذ شبکه و مختصات دکارتی آسان بود. اما دایره ها به روشی دیگر احتیاج دارند، به خصوص که ما الگوریتمی لازم داریم که روی هر پیکسل به صورت جدا اجرا می‌شود. یک راه این است که مختصات را تغییر دهیم و از تابعstep() برای ترسیم دایره استفاده کنیم.

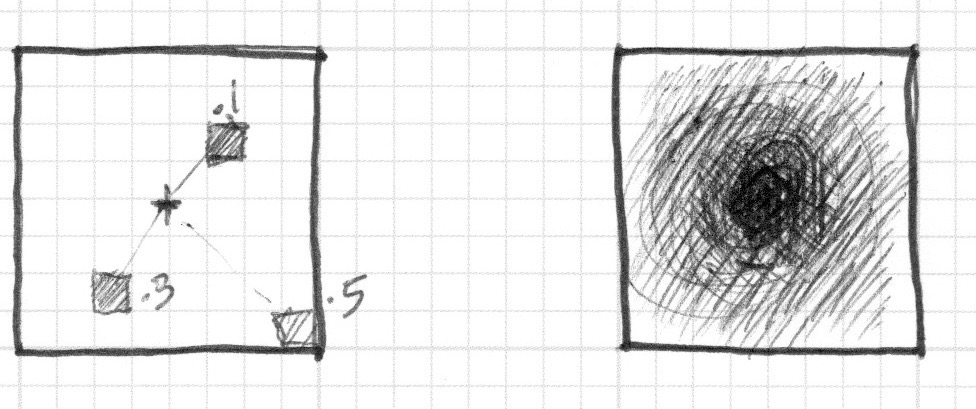
چگونه? بیایید برگردیم به کلاس ریاضی و کاغذ شبکه ای مان, زمانی که پرگار را به اندازه شعاع دایره مان باز می‌کردیم, یکی از نقاط پرگار را به وسط دایره فشار می‌دادیم و بقیه را در امتداد آن دایره می‌چرخاندیم.

در شیدر ما برای هر پیکسل این سوال را می‌پرسیم، که آیا این پیکسل یا همان ترد در داخل منطقه دایره مورد نظر ما هست یا خیر. این کار را با محاسبه فاصله پیکسل تا مرکر دایره می‌توان انجام داد..

راه های زیادی برای محاسبه فاصله وجود دارد. راحت ترین آن استفاده از distance() است, که همان طول length() بین دو نقطه را محاسبه می‌کند (در مثال ما فاصله بین پیکسل مورد نظر و مرکز دایره). تابع length() کوتاه شده hypotenuse equation است، از جزر (sqrt()) استفاده می‌کند.

برای محاسبه فاصله می‌توانید از هر کدام از distance(), length() یا sqrt() استفاده کنید. کد زیر حاوی هر 3 این عملکرد ها است، همانطور که پیش بینی می‌کنید هر یک نتیجه مشابهی را بر می‌گردانند.

• خطوط را از حالت کامت خارج کنید و روش های دیگر را کامنت کنید تا نتیجه یکسان را مشاهده کنید .

در مثال قبلی فاصله پیکسل تا مرکز کنوس میزان روشنایی را ترسیم میکند. هرچه پیکسل به مرکز نزدیکتر باشد، مقدار آن تیره و کمتر است. توجه کنید که مقادیر خیلی زیاد نمی‌شوند زیرا فاصله یک پیکسل از مرکز حداکثر کمی بیش از 0.5 است. این را در نظر بگیرید و فکر کنید:

• چه چیزی از آن می‌توانید استنباط کنید?

• چگونه از این روش برای کشیدن دایره می‌توان استفاده کرد?

• کد بالا را طوری تغییر دهید که تمام گرادیان دایره داخل کنوس باشد..

Distance field

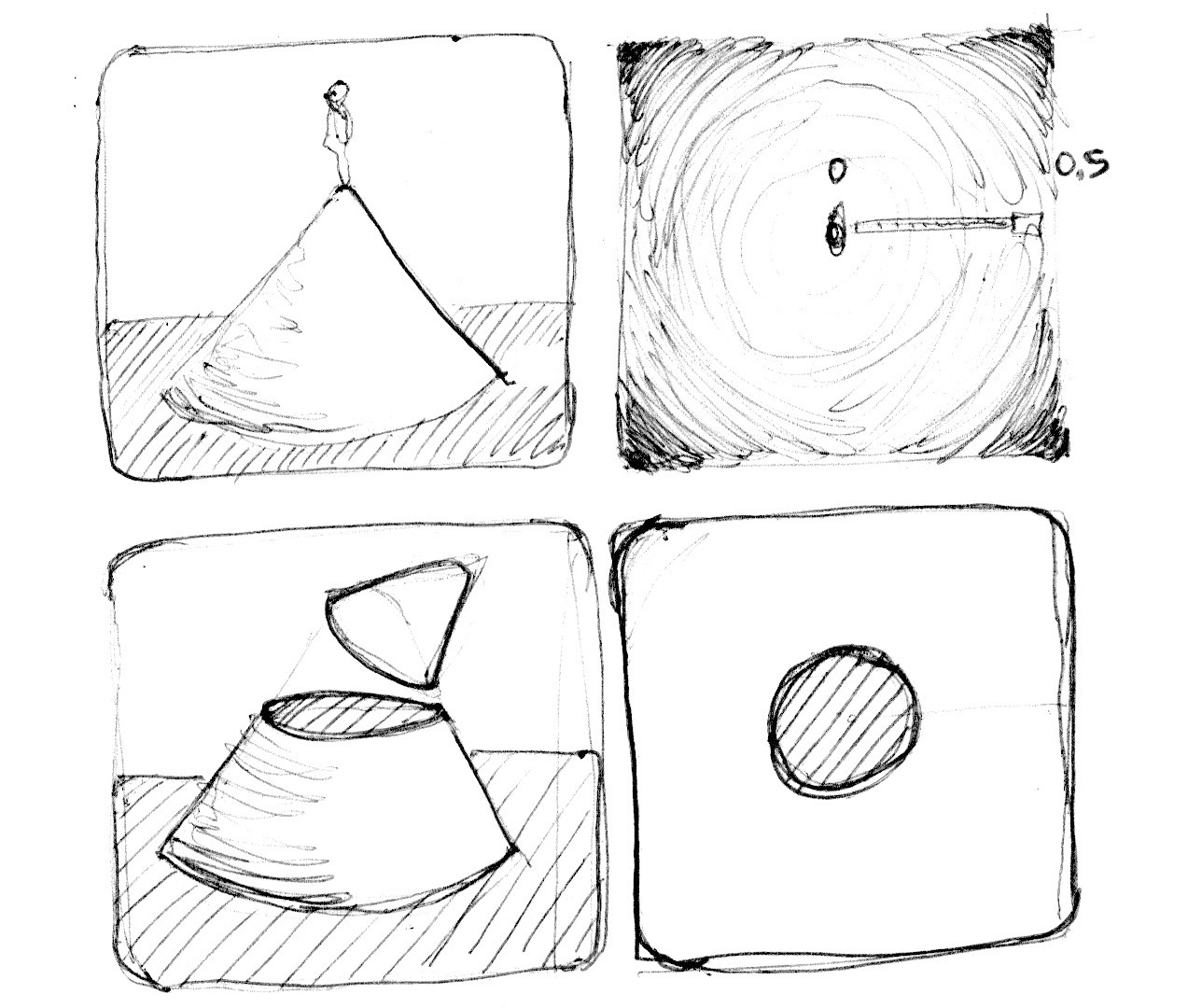
می‌توان مثال بالا را مانند یک نقشه ارتفاع در نظر گرفت، جایی که هر چه تاریک تر باشد یعنی بلند تر است. گرادیان تولید شده الگویی مانند مخروط را به ما نمایش می‌دهد، خود را در بالای آن مخروط در نظر بگیرید، فاصله افقی تا لبه ی مخروط برابر 0.5 است، این عدد از همه جهات ثابت است، با انتخاب محل برش مخروط، می‌توان یک دایره در آن سطح بدست آورد.

اساس ما برای ساخت اشکال از تفسیر مجدد فضا در این مثال بر اساس فاصله تا مرکز، استفاده می‌کنیم. این تکنیک بعنوان“distance field” و به روش های گوناگون در outLine فونت ها تا گرافیک سه بعدی از آن استفاده می‌شود.

تمرین های زیر را انجام دهید:

• از تابع step() استفاده کنید تا همه چیز بیش تر از 0.5 را به سفید و کمتر از 0.5 را به سایه 0.0 تبدیل کند.

• رنگ بکگراند و فورگراند را عوض کنید.

• از تابعsmoothstep(), با مقادیر مختلف استفاده کنید تا یک مرز نرم برای دایره بسازید.

• وقتی از نتیجه راضی بودید، از آن یک تابع بسازید تا بعدا بتوانبد استفاده کنید.

• به دایره رنگ اضافه کنید.

• آیا می‌تواندی مانند یک قلب تپنده، دایره خود را کوچک و بزرگ کنید؟ می‌تواندی از انیمیشن های فصل قبل الهام بگیرید.

• آیا می‌توانید دایره را حرکت دهید؟ اضافه کردن دایره های بیشتر چطور؟

• اگر فیلد فاصله را با عملکرد های دیگر ترکیب کنید چه اتفاقی می‌افتد؟

pct = distance(st,vec2(0.4)) + distance(st,vec2(0.6));
pct = distance(st,vec2(0.4)) * distance(st,vec2(0.6));
pct = min(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = max(distance(st,vec2(0.4)),distance(st,vec2(0.6)));
pct = pow(distance(st,vec2(0.4)),distance(st,vec2(0.6)));

• با استفاده از این تکنیک سه ترکیب بسازید، اگر به حالت انیمیشنی باشد که چه بهتر!

جعبه ابزار

بار محاسباتی تابع sqrt() و توابعی که از آن استفاده می‌کنند، زیاد است. این یک راه دیگر برای ساخت فیلد فاصله دایره ای با استفاده از ضرب داخلی dot() است.

فواید دیگر فیلد(میدان) فاصله

با استفاده از فیلد فاصله تقریبا می‌توان هر چیزی کشید. مشخصا هر چه شکل پیچیده تر باشد، معادله آن پیچیده تر خواهد بود، اما وقتی فرمول فیلد فاصله برای رسم یک شکل را بدست آورید، خیلی ساده میتوان آن را با افکت های دیگر ترکیب یا اضافه کرد، مانند لبه های نرم یا outLine ها . برای همین استفاده از فیلد فاصله در رندر کردن فونت ها بسیار رایج است, مانند Mapbox GL Labels, Matt DesLauriers Material Design Fonts و as is described on Chapter 7 of iPhone 3D Programming, O’Reilly.

نگاهی به کد زیر بیاندازید.

برای شروع مختصات را به مرکز انتقال دادیم و برای مپ کردن مقادیر بین 1 و -1 آن را به نصف فشرده کردیم. همچنین در خط 24 ما فیلد فاصله را با استفاده از تابع fract() نشان می‌دهیم، این تابع پترن ساخته شده را راحتر به نماش می‌گذارد. الگوی میدان فاصله مانند حلقه های باغ zen مکررا تکرار می‌شوند.

بیایید نگاهی به فرمول فاصله فیلد در خط 19 بیاندازیم. در آنجا ما فاصله تا مکان (.3و.3) را در هر چهار ربع مختصات محاسبه می‌کنیم (به همین علت از قدر مطلق abs() استفاده کردیم).

اگر خط 20 را از کامنت خارج کنید، ترکیب تابع فاصله با این چهار نقطه به همراهmin() استفاده کردیم و الگویی جالب را بدست آوردیم.

حال خط 21 را از کامنت خارج کنید، همان کار را انجام می‌دهیم اما اینبار توسط تابع max() . نتیجه مستطیل هایی با گوشه های خمیده است. توجه کنید که حلقه ها هر چه دورتر هستند، نرم تر می‌شوند.

خطوط 27 تا 29 را یک به یک از حالت کامنت خارج کنید و کاربرد های مختلف الگوی فاصله فیلد را درک کنید..

اشکال قطبی

در فصل رنگ ها با محاسبه شعاع و زاویه مختصات دکارتی را به قطبی تبدیل کردیم، از فرمول زیر استفاده کرده بودیم:

vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);

در اول این فصل از قسمتی از این فرمول برای رسم دایره استفاده کردیم. با استفاده از length() فاصله پیکسل تا مرکز را محاسبه می‌کردیم. حالا که در مورد فیلد فاصله می‌دانیم، می‌توان از راه دیگری برای رسم اشکال در مختصاب قطبی استفاده کرد‌.

این روش کمی محدود کننده، اما بسیار ساده است. این روش از تغییر شعاع دایره بسته به زاویه برای رسم اشکال مختلف استفاده می‌کند. اما چگونه؟ با استفاده از توابع شکل دهی.

در خطوط 21 تا 25 مثال زیر همان توابع در مختصات دکارتی را در مختصات قطبی مشاهده می‌کنید. یک به یک خط ها را از حالت کامنت خارج کنید، به رابطه بین مختصات های مختلف توجه کنید.

سعی کنید:

• این اشکال را انیمیت کنید.
• توابع مختلف شکل دهی را ترکیب کنید تا برشی وسط شکل بتوانید ایجاد و اشکالی مثل گل، دانه برف و چرخ دنده ایجاد کنید.
• از تابع plot() که در فصل توابع شکل دهی ساختیم استفاده کنید تا فقط حد فاصل دور اشکال را رسم کنید.

ترکیب قدرت ها

اکنون که با استفاده از atan() یاد گرفتیم چگونه شعاع دایره را با استفاده از زاویه آن تنظیم کنیم و اشکال مختلف بسازیم, حال می‌توان از atan() با فیلد فاصله استفاده کرد و تکنیک های که یاد گرفیم روی آن استفاده کرد..

این ترفند از لبه های چند ضلعی برای ساخت فیلد فاصله با استفاده از مختصات قطبی استفاده می‌کند. این کد از Andrew Baldwin را نگاهی بیاندازید.

• با استفاده از این مثال تابعی ایجاد کنید، که مقدار گوشه ها و موقعیت یک شکل را دریافت و یک فیلد فاصله برگرداند.

• فیلد های فاصله را با استفاده از min() و max() با هم ترکیب کنید.

• یک لوگو هندسی را انتخاب کنید، و سعی کنید آن را با استفاده از فیلد فاصله بسازید.

تبریک! بخش سختی را گذراندید! کمی استراحت کنید و اجازه دهید این مفاهیم جا بیوفتد، ساخت اشکال در نرم افزار Processing آسان است، ولی اینجا خیر. در سرزمین شیدر ها طراحی شکل پیچیده است، و سازگاری با این الگوی جدید می‌تواند طاقت فرسا باشد!

در آخر این صفحه به شما PixelSpirit Deck معرفی شده. این کارت ها به شما توابع شکل دهی را بخوبی یاد می‌دهند. از آن ها در طرح ها و شیدر های خودتان استفاده کنید. این دسته کارت دارای یک منحنی یادگیری تدریجی است. بنابر این تمرین کردن یک کارت در هر روز می‌تواند تا 30 روز شما را به چالش بکشد.

اکنون که می‌دانید چگونه اشکال را رسم کنید، مطمئنم ایده های جدید در ذهنتان ایجاد می‌شود. در فصل بعدی، نحوه حرکت، چرخش و مقیاس پذیری اشکال را خواهید آموخت. و امکان ترکیب آنان را خواهید داشت.