mirror of https://github.com/patriciogonzalezvivo/thebookofshaders synced 2024-11-08 01:10:27 +00:00

MITI67 468fc026b0 new: german translation

2016-11-10 19:20:44 +01:00

16 KiB

Raw Blame History

Algorithmisches Zeichnen

Modellierungsfunktionen

Dieses Kapitel könnte auch die Überschrift „Mr. Miyagi's Zaun- Lektion“ tragen, in Anspielung auf den Film „Karate Kid“ aus dem Jahre 1984. Bislang haben wir die normalisierte Position von x und y auf den roten und grünen Farbkanal des jeweiligen Punktes abgebildet. Wir haben dazu eine Funktion gebaut, die im Wesentlichen einen zweidimensionalen Vektor (X und Y) entgegennimmt und einen vierdimensionalen Vektor (Rot, Grün, Blau und Alpha) zurückliefert. Aber bevor wir damit fortfahren, Daten zwischen verschiedenen Dimensionen zu transformieren, müssen wir mit einfacheren Aufgaben beginnen. Und zwar mit viel einfacheren Aufgaben. Ich meine damit das Verständnis eindimensionaler Funktionen. Desto mehr Zeit und Energie Du darauf verwendest, desto stärker wird dein Shader-Karate sein.

Die folgende Codestruktur ist unser Zaun, an dem wir in Anlehnung an die Geschichte von „Karate Kid“ üben werden. Wir visualisieren damit den normalisierten Wert der X-Ordinate (st.x) auf zweierlei Weise: einmal in Form der Helligkeit (beachte den weichen, schrittweisen Übergang von Schwarz zu Weiß) und außerdem indem wir die Werte in Form einer grünen (Funktions-) Linie darstellen (der jeweilige X-Wert wird dabei eins-zu-eins auf den Y-Wert abgebildet). Halte Dich dabei bitte nicht zu lange mit der plot()-Funktion auf, denn darauf werden wir gleich noch im Detail eingehen.

Ein kurzer Hinweis: Der Konstruktor des vec3-Datentyps „versteht“, wenn Du allen drei Farbkanälen durch die Angabe eines einzigen Parameters diesen einen gleichen Wert zuweisen willst. In diesem Fall erhält man immer einen Grauton zwischen Schwarz (0.0, 0.0, 0.0) und Weiß (1.0, 1.0, 1.0).

Ebenso versteht der Konstruktor des vec4-Datentyps, wenn Du einen vierdimensionalen Vektor aus einem dreidimensionalen Vektor erzeugen willst. Der dreidimensionale Vektor verkörpert in diesem Fall den RGB-Farbwert, der zusätzliche Parameter den Wert für den Alpha-Kanal, also die Deckkraft. Dies geschieht hier in den Programmzeilen 20 und 26.

Dieser Programmcode ist Dein Zaun, an dem Du das Streichen bzw. Malen üben kannst. Es ist wichtig, dass Du Dir den Code genau anschaust und ihn verstehst. Denn die darin enthaltenen Konzepte, wie etwa die Normalisierung von x und y auf Werte zwischen 0.0 und 1.0, werden uns weiterhin begleiten.

Die hier genutzte Eins-zu-Eins-Abbildung zwischen x und y (in diesem Fall als Helligkeit genutzt) wird als lineare Interpolation bezeichnet. Davon abweichend können wir auch unterschiedliche mathematische Funktionen nutzen, um der Linie eine andere Form zu geben. So können wir zum Beispiel x hoch 5 einsetzen, um eine geschwungene, steil ansteigende Kurve zu erzeugen.

Interessant, nicht wahr? Versuche einfach einmal, in der Zeile 22 andere Exponenten wie beispielsweise 20.0, 2.0, 1.0, 0.0, 0.2 und 0.02 einzusetzen. Das Verständnis zwischen dem Exponenten und den daraus resultierenden Werten wird Dir sicher weiterhelfen. Schließlich ist es der geschickte Einsatz dieser und anderer mathematischer Funktionen, die Dir bei der Shader-Programmierung unglaubliche Möglichkeiten eröffnen.

pow() ist eine eingebaute mathematische Funktion von GLSL. Daneben gibt es noch viele weitere. Die meisten davon können sehr schnell in der Hardware der Grafikkarte ausgeführt werden. Ihr geschickter Einsatz beschleunigt deshalb die Ausführung Deiner Shader.

Ersetze die Funktion pow in der Zeile 22 durch eine andere Funktion und beobachte das Resultat. Probiere zum Beispiel die folgenden Funktionen aus: exp(), log() und sqrt(). Einige dieser Funktionen erzeugen interessantere Ergebnisse, wenn man sie in Verbindung mit einem Vielfachen oder einem Bruchteil der Kreiszahl pi nutzt. In der Programmzeile 8 findest Du deshalb ein Makro, dass das Symbol PI innerhalb des Programmcodes durch den zugehörigen Wert 3.14159265359 ersetzt.

Step und Smoothstep

GLSL bringt auch einige einzigartige Interpolationsfunktionen mit, die durch die Hardware beschleunigt werden.

Die Interpolationsfunktion step() nimmt zwei Argumente entgegen: Das erste verkörpert den Schwellenwert, während das zweite Argument den Wert darstellt, der mit diesem Schwellenwert verglichen werden soll. Liegt dieser Wert unterhalb des Schwellenwerts, liefert die Funktion 0.0 zurück, bei jedem Wert größer oder gleich dem Schwellenwert hingegen 1.0.

Ändere im folgenden Programmcode doch einfach einmal den Schwellenwert in Zeile 20 und beobachte, was dann passiert.

Die zweite eingebaute Interpolationsfunktion trägt den Namen smoothstep(). Sie interpoliert einen Wert, sofern sich dieser innerhalb eines angegebenen Wertbereichs befindet. Die ersten zwei Argumente stellen dabei die untere und die obere Schwelle dieses Wertebereichs dar, während das dritte Argument den zu interpolierenden Wert verkörpert.

Die Funktion liefert 0.0 zurück, wenn der zu interpolierende Wert unterhalb des genannten Schwellenwerts liegt, also kleiner als das erste Argument ist. Analog dazu liefert sie 1.0 zurück, wenn der zu interpolierende Wert größer als der obere Schwellenwert ist. Befindet sich der zu interpolierende Wert jedoch innerhalb der gegebenen Spanne, wird ein Wert zwischen 0.0 und 1.0 zurückgeliefert, je nachdem wie nahe sich der Wert am oberen oder unteren Ende der Spanne befindet. Genau in der Mitte lautet das Ergebnis 0.5.

Wie das folgende Programm zeigt, ist das Ergebnis jedoch nicht vollständig linear, sondern am oberen und unteren Ende des Wertebereichs etwas „abgerundet“. Dadurch wird in den Randbereichen bewusst ein etwas weicherer Übergang erzielt, falls sich weitere interpolierte Werte anschließen.

Im obigen Beispiel nutzen wir die smoothstep()-Funktion innerhalb der plot()-Funktion, um die grüne Linie zu erzeugen, die die Ergebnisse aus der Y-Berechnung in Zeile 20 darstellt. Siehst Du, wie diese grüne Linie nach oben und unten jeweils ein wenig ausfedert und sanft in den Hintergrund übergeht? Das erreichen wir, indem wir in Zeile 12 und 13 zwei Aufrufe von smoothstep() miteinander verbinden. Schau Dir die folgende Berechnung an und setze sie in die Zeile 20 ein.

    float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);

Die Formel entspricht dem Vorgehen innerhalb der plot()-Funktion. Sie symbolisiert, wie plot() genau in der Mitte (auf dem gegebenen Y-Wert) ein volles Grün erzeugt (Rückgabewert 1.0), während bei Werten darunter und darüber ein weicher Übergang zur Hintergrundfarbe erfolgt (Rückgabewerte von 1.0 langsam absteigend zu 0.0).

Sinus und Cosinus

Wenn man mathematische Funktionen nutzen möchte, um Grafiken zu animieren, in eine geschwungene Form zu bringen oder sanft ein- und auszublenden, gibt es nichts Besseres, als sich mit Sinus und Cosinus anzufreunden.

Diese beiden trigonometrischen Funktionen sind so praktisch wie ein Schweizer Offiziersmesser, wenn es darum geht, Kreise zu konstruieren. Es ist wichtig zu verstehen, wie sich die beiden Funktionen einzeln verhalten und wie man sie gemeinsam nutzen kann. Kurz gesagt, bei einem gegebenen Winkel (in Form eines Bogenmaßes) liefern sie die korrekte x- (Cosinus) und y- (Sinus) Ordinate für die Position des zugehörigen Punktes auf einem Einheitskreis mit dem Radius 1. Weil sich die zurückgelieferten Funktionsergebnisse dabei immer dynamisch zwischen -1.0 und 1.0 oszillieren, sind diese Funktionen ein ungeheuer praktisches Werkzeug für vielerlei Aufgaben.

Es ist nicht ganz leicht, alle Zusammenhänge zwischen trigonometrischen Funktionen auf der einen Seite und Kreisen auf der anderen Seite zu beschreiben. Die obige Animation zeigt jedoch sehr schön die oben zitierte Rolle von Sinus und Cosinus bei der Erzeugung eines Einheitskreises.

Schau Dir die Sinuswelle genau an und beobachte, wie der daraus abgeleitete Wert für die Y-Ordinate auf dem Einheitskreis sanft zwischen +1 und -1 oszilliert. Und mit der Cosinuswelle erzeugen wir die zugehörige X-Ordinate.

Wie wir in dem zeitbasierten Beispiel im vorangegangenen Kapitel gesehen haben, lässt sich dieses rhythmische Verhalten von sin() gut nutzen, um bestimmte Werte und Eigenschaften zu animieren. Wenn Du diesen Text in einem Internet-Browser liest, wirst du feststellen, dass Du die obige Formel y=sin(x); editieren kannst, um zu sehen, wie sich die Funktionskurve dadurch ändert. (Hinweis: Bitte nicht das Semikolon am Ende der Zeile vergessen, sonst gibt es einen Syntaxfehler.)

Probiere die folgenden Übungen aus und beobachte, was daraufhin geschieht:

Addiere die Zeit (u_time) zu x hinzu, bevor Du aus der Summe den sin berechnest. Verinnerliche die daraus entstehende Bewegung entlang der x-Achse.
Multipliziere x mit PI, bevor Du den sin berechnest. Beobachte, wie sich die Phasenlänge auf jeweils 2 Einheiten entlang der X-Achse verkürzt und sich die Schwingung dann wiederholt. Dadurch verdoppelt sich also die Frequenz.
Multipliziere die Zeit (u_time) mit x, bevor Du daraus den sin berechnest. Du wirst sehen, wie die einzelnen Wellen so weit zusammengedrückt werden, dass das Ergebnis wie ein unidentifizierbares Rauschen wirkt.
Addiere den Wert 1.0 zum Ergebnis von sin(x) hinzu und beobachte, wie sich die Welle dadurch nach oben verschiebt und jeweils zwischen den Werten von 0.0 und 2.0 oszilliert.
Multipliziere sin(x) mit 2.0. Du wirst feststellen, dass sich die Amplitude der Schwingung (die Minimal- und Maximalwerte) verdoppelt.
Lass den absoluten Wert (abs()) von sin(x) berechnen. Der entstehende Graph erinnert an die Spur eines hüpfenden Balls, nicht wahr?
Lass nur den Nachkommateil (fract()) des Resultats von sin(x) berechnen.
Addiere jeweils den höheren Integer-Wert (ceil()) von sin(x) und den kleineren Integer-Wert (floor()) von sin(x), um eine digitale Welle zwischen 1 und -1 zu erhalten.

Einige besonders nützliche Funktionen

Am Ende der letzten Übung haben wir einige neue Funktionen eingeführt. Jetzt ist es an der Zeit, mit diesen Funktionen zu experimentieren, indem Du Schritt für Schritt die Kommentarzeichen aus den folgenden Programmzeilen entfernst. Lerne diese Funktionen kennen und beobachte, wie sie funktionieren. Du wirst Dich vielleicht fragen, warum? Eine Google-Suche nach „generativer Kunst“ bzw. „generative art“ wird Dir diese Frage schnell beantworten. Denke daran, dass diese Funktionen wie der Zaun aus „Karate Kid“ sind. Noch bewegen wir uns nur in einer Dimension, aufwärts und abwärts. Aber bald schon geht es damit in zwei, drei und vier Dimensionen!

Fortgeschrittene formgebende Funktionen

Golan Levin hat eine großartige Dokumentation über komplexe formgebende Funktionen verfasst, die für unsere Zwecke extrem hilfreich ist. Indem Du einen Teil dieser Funktionen nach GLSL portierst, schaffst Du Dir eine wertvolle Sammlung an Codeschnipseln.

Genau wie Küchenchefs Gewürze und exotische Zutaten sammeln, entwickeln Digitalkünstler und kreative Entwicker häufig eine Liebe für bestimmte formgebenden Funktionen.

Inigo Quiles stellt eine großartige Auswahl an nützlichen Funktionen vor. Wenn Du diesen Artikel gelesen hast, dann werfe einen Blick auf die folgenden Übertragungen dieser Funktionen nach GLSL. Beobachte aufmerksam die kleinen, aber erforderlichen Anpassungen wie etwa den Punkt (".") bei Fließkommazahlen und die Umsetzung der Funktionsnamen von C auf GLSL; so heißt es in GLSL beispielsweise pow() statt powf() wie in C:

Um Deine Motivation zu erhalten, hier ein elegantes Beispiel (entwickelt von Danguafer) für die Meisterschaft im Karate der formgebenden Funktionen.

Im nächsten Kapitel werden wir neue Schrittfolgen für unser „Karate“ lernen. Zunächst beim Mischen von Farben, dann beim Malen von Formen.

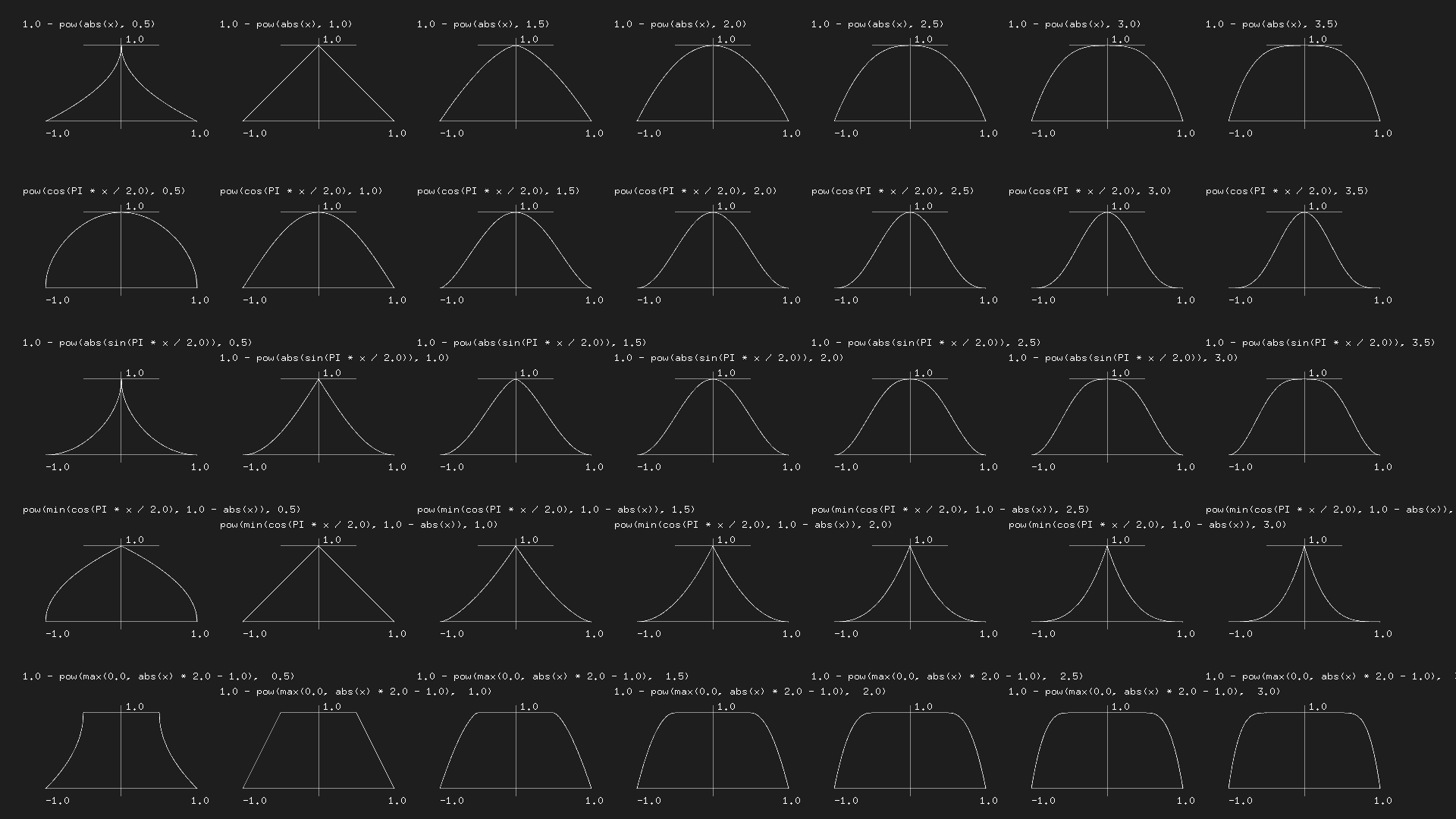
####Übung

Wirf einen Blick auf die folgende Tabelle mit Gleichungen, die von Kynd erstellt wurde. Schau Dir an, wie er Funktionen und ihre Eigenschaften kombiniert, um Werte zwischen 0.0 und 1.0 zu erhalten. Jetzt ist ein guter Moment, um mit diesen Funktionen ein wenig zu experimentieren. Denn je mehr Du in dieses Denken hineinwächst, desto besser wird Dein Karate sein.

####Für Deine Werkzeugsammlung

Hier kommen einige Tools, die es Dir erleichtern werden, diese Art von Funktionen grafisch zu visualisieren.

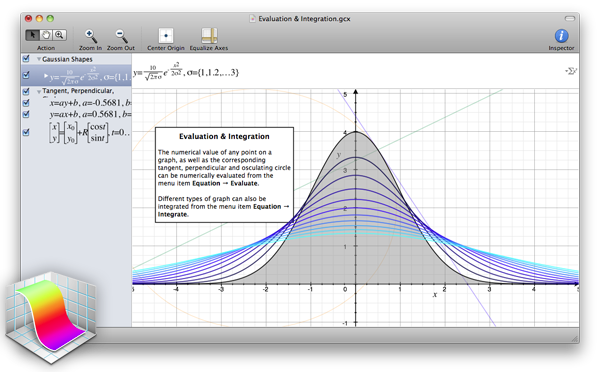
Grapher: Wenn Du einen Computer mit MacOS hast, gib bei der Suche mit Spotlight grapher ein, und Du wirst dieses superpraktische Tool finden.

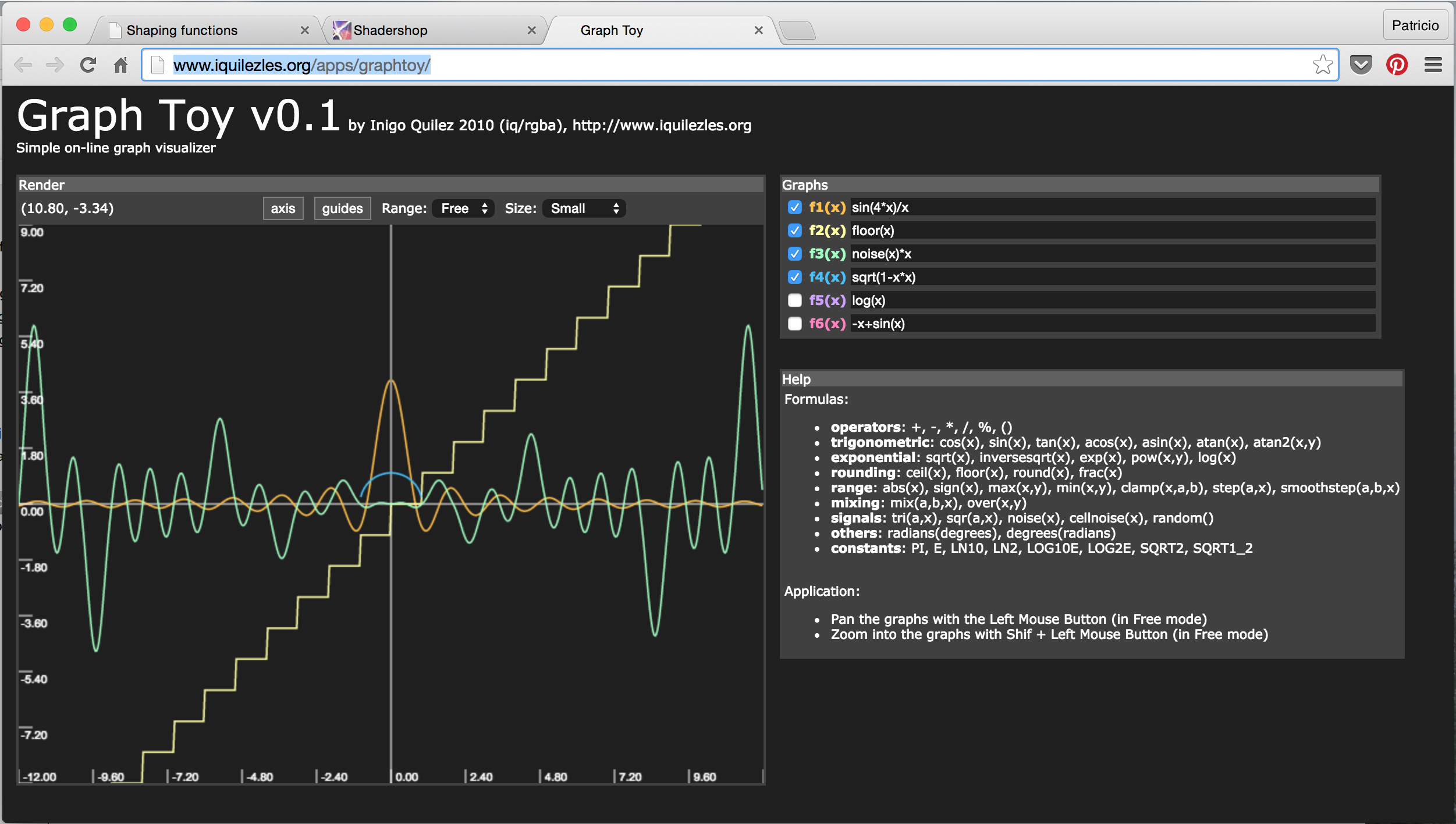
GraphToy: Einmal mehr ein Werkzeug von Inigo Quilez, mit dem man GLSL-Funktionen in WebGL darstellen kann.

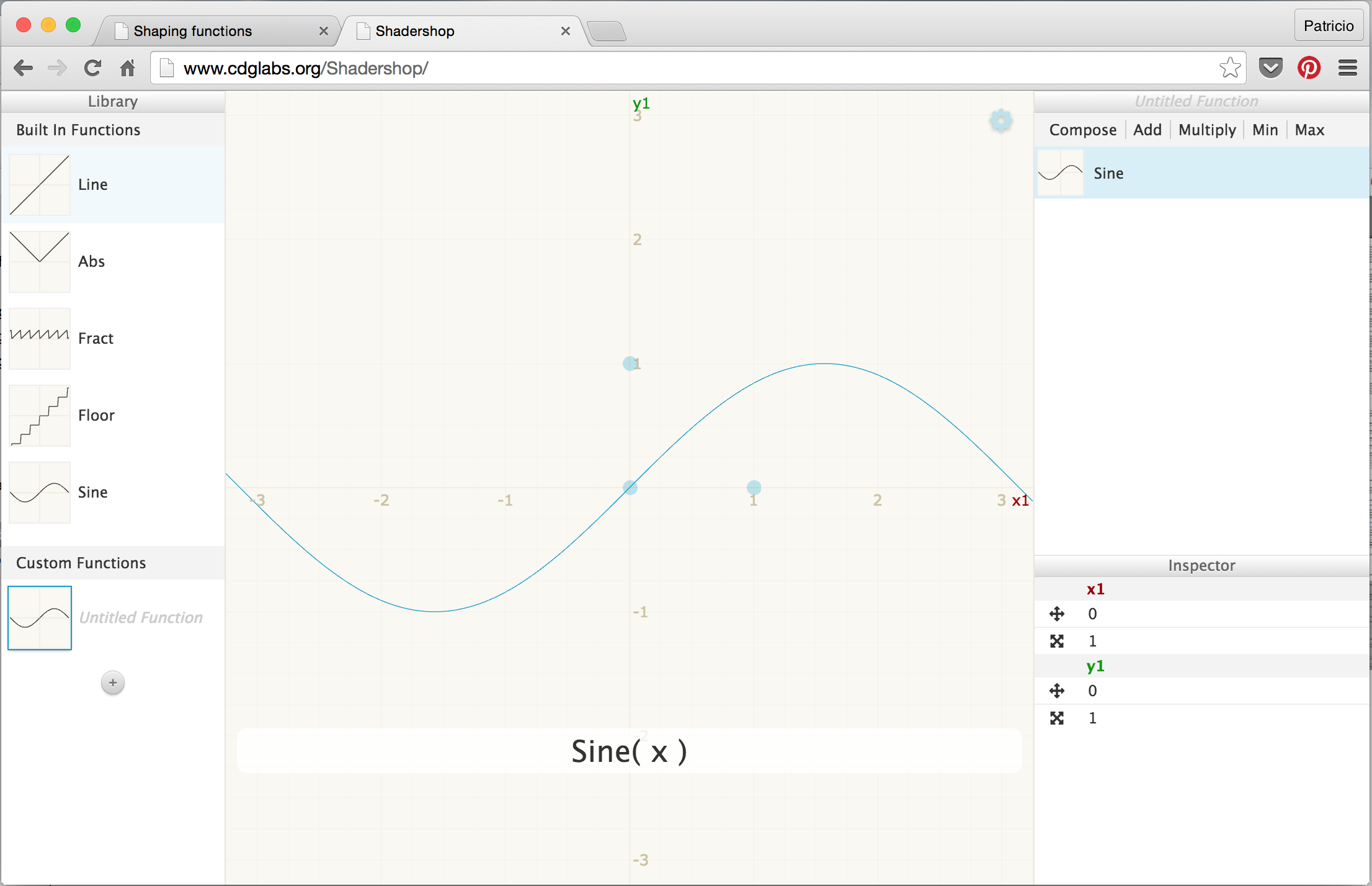
Shadershop: Dieses großartige Werkzeug von Toby Schachman zeigt Dir auf intuitive und grafisch faszinierende Weise, wie Du komplexe Funktionen entwickeln kannst.

16 KiB Raw Blame History