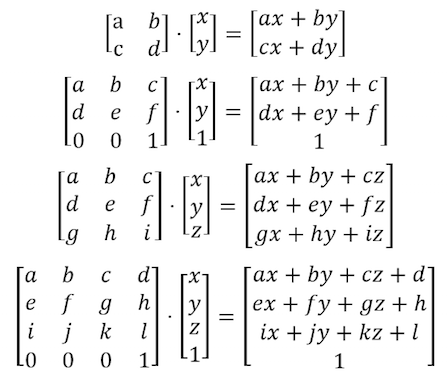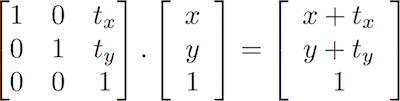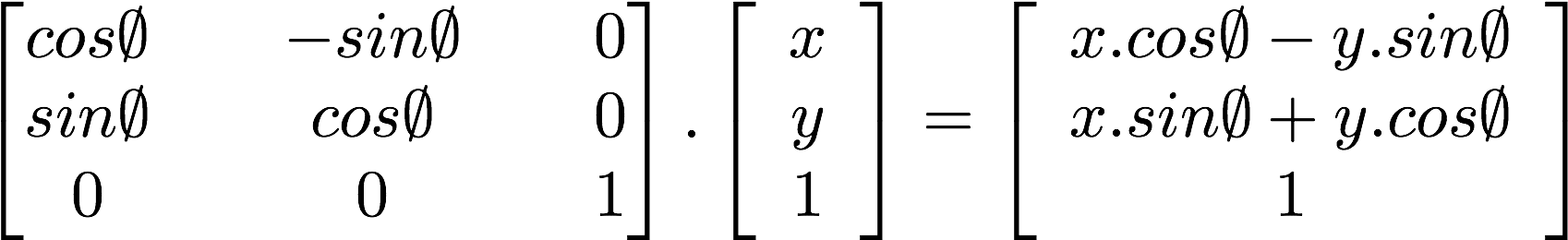thebookofshaders/08/README-pt.md

Matrizes 2D

Translação

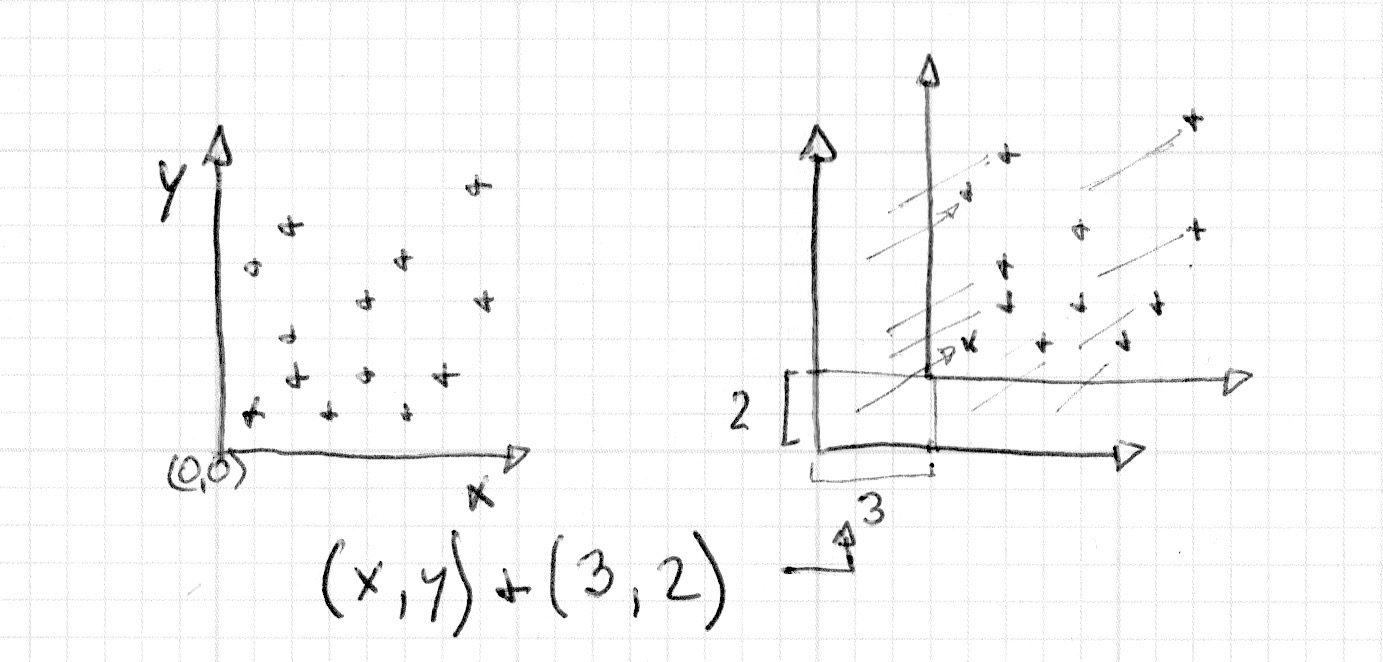
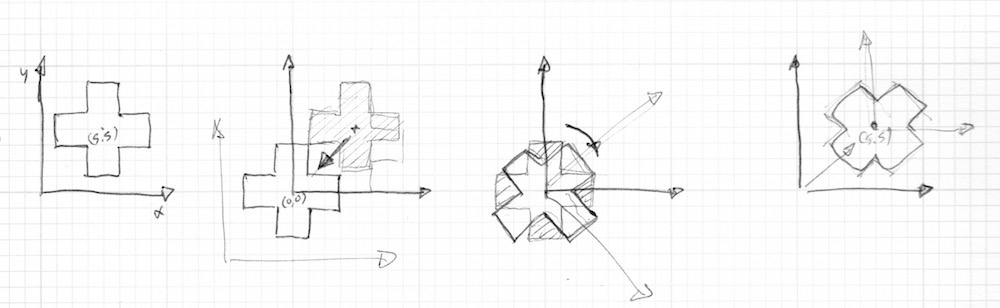
No capítulo anterior, nós aprendemos como criar algumas formas - o truque para mover estas formas é mover o próprio sistema de coordenadas. Nós fazemos isso simplesmente adicionando um vetor às variáveis st que contem a localização de cada fragmento. Isso fará com que todo o espaço de coordenadas se mova.

Isso é mais fácil de enxergar do que explicar, veja você mesmo:

• Descomente as linhas 35 do código abaixo e veja como o próprio espaço se move.

Agora implemente os seguintes exercícios:

• Usando u_time junto com a modelagem de função, mova a pequena cruz de uma forma interessante. Procure por uma específica qualidade de movimento que você se interessa e tente fazer com que a cruz se mova da mesma forma. Se lembrando de algo suave do "mundo real" primeiramente pode ser útil - Pode ser as ondas que vem e vão de um pêndulo, uma bola quicando, um carro acelerando uma bicicleta parando.

Rotações

Para rotacionarmos objetos, também precisamos mexer todo o sistema espacial. Para isso, nós iremos usar uma matriz. Uma matriz é um conjunto organizado de números em linhas e colunas. Vetores são multiplicados por matrizes seguindo um preciso conjunto de ordens para modificar os valores do vetor em uma forma particular.

GLSL tem um suporte nativo para matrizes de duas, três e quatro dimensões: mat2 (2x2), mat3 (3x3) e mat4 (4x4). GLSL também suporta multiplicação de matrizes (*) e uma função específica para matriz (matrixCompMult()).

Baseado em como matrizes se comportam, é possível construir matrizes para produzir comportamentos específicos. Por exemplo, nós podemos usar matriz para transladar um vetor:

E mais interessante ainda, podemos usar uma matriz para rotacionar um sistema de coordenadas:

Dê uma olhada no seguinte código para uma função que constrói uma matriz de rotação bidimensional. Esta função segue a formula acima para vetores de duas dimensões rotacionarem as coordenadas em torno do ponto vec2(0.0).

mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

De acordo com o jeito que estamos desenhando formas, isto não é exatamente o que queremos. Nossa forma de cruz está desenhada no centro do canvas, que corresponde a posição vec2(0.5). Então, antes de rotacionarmos o espaço, nós precisamos mover a forma, do centro para a coordenada vec2(0.0), rotacionar o espaço, e então, finalmente, move-la de volta ao seu lugar original.

Isso se parece com o seguinte código:

Tente os seguintes exercícios:

• Descomente a linha 45 do código acima e preste atenção no que acontece.

• Comente as translações antes e depois da rotação, nas linhas 37 e 39, e observe as consequencias.

• Use rotações para melhorar a animação que você simulou no exercício de translação.

Escala

Nós vimos como matrizes são usadas para mover e rotacionar objetos no espaço. (Ou mais precisamente, transformar o sistema de coordenadas para rotacionar e mover os objetos.) Se você já usou um software de modelagem 3D ou o as funções de matrizes push e pop em Processing, você verá que matrizes também podem ser usadas para escalonar o tamanho de um objeto.

Se baseando na fórmula anterior, podemos descobrir como fazer uma matriz 2D de escala:

mat2 scale(vec2 _scale){
    return mat2(_scale.x,0.0,
                0.0,_scale.y);
}

Tente os seguintes exercícios para entender mais profundamente como isso funciona.

• Descomente a linha 42 do código acima para ver coordenadas espaciais serem escalonadas.

• Veja o que acontece quando você comenta as translações antes e depois de escalonar nas linhas 37 and 39.

• Tente combinar a matriz de rotação junto com a matriz de escala. Note que a ordem das matrizes importa. Multiplique primeiramente pela matriz e então, multiplique os vetores.

• Agora que você sabe como desenhar diferentes formas, e mover rotacionar e escalona-las, stá na hora de fazer uma ótima composição. Projete e construa uma fake UI or HUD (heads up display)](https://www.pinterest.com/patriciogonzv/huds/). Use os seguintes exemplos do Shadertoy Ndel como referência e inspiração.

Outros usos para matrizes : Cores YUV

YUV é um sistema de codificação de cores usado para transmissão analógica de fotos e vídeos que leva em consideração a percepção humana para reduzir a largura de banda dos componentes de crominância.

O código a seguir é uma interessante oportunidade de usar operações de matrizes em GLSL e transformar as cores de um modo para outro.

Como você pode ver, nós estamos tratando cores como vetores quando multiplicamos elas pelas matrizes. Desta forma podemos "mover" os valores.

Neste capítulo, nós aprendemos como usar transformações de matrizes para mover, rotacionar e escalonar vetores. Estas transformações serão essenciais para criar as composições além das formas que aprendemos no capítulo anterior. No próximo capítulo, nós vamos aplicat tudo que aprendemos para criar lindos padrões procedurais. Você irá descobrir que programar repetições e variações podem ser uma empolgante prática.