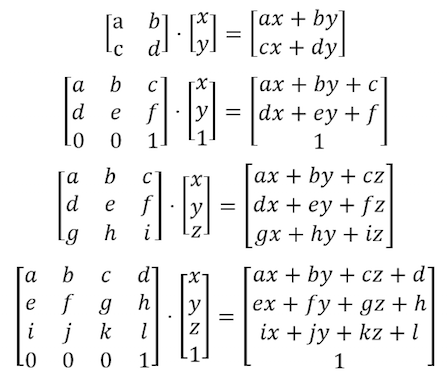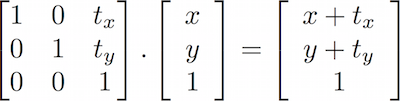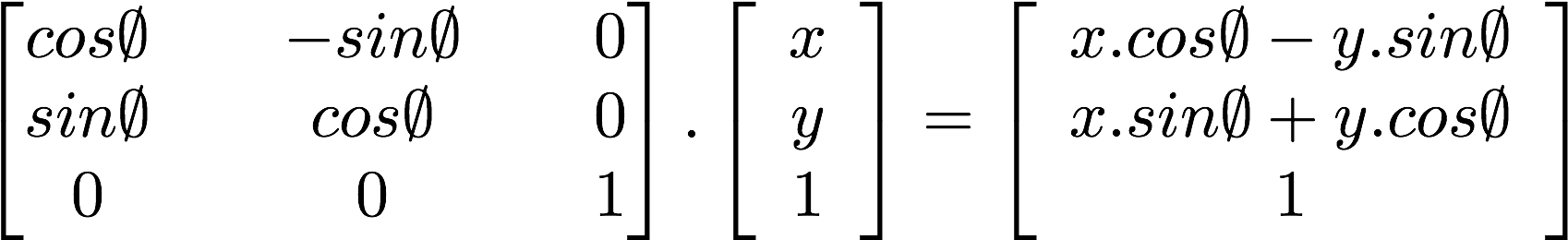thebookofshaders/08/README-ru.md

Двумерные матрицы

Перенос

В предыдущей главе мы научились рисовать фигуры. А для того, чтобы передвинуть фигуру, достаточно передвинуть саму систему координат. Этого можно добиться всего лишь прибавление вектора к переменной st, содержащей положение фрагмента. Это приводит к перемещению всей системы координат в пространстве.

Это проще увидеть, чем объяснить, поэтому смотрите сами:

• Раскомментируйте строку 35 в коде ниже чтобы увидеть как движется само пространство.

Теперь попробуйте выполнить следующее:

• Используйте u_time и функции формы для перемещения креста каким-нибудь нестандартным способом. Придумайте движение, которое кажется вам интересным, и заставьте крест двигаться таким образом. Попробуйте срисовать что-нибудь из реального мира, например прибегающие и отступающие волны, движение маятника, подпрыгивающий мячик, ускоряющуюся машину или тормозящий велосипед.

Повороты

Для вращения объектов нам снова придётся поворачивать всё пространство. Для этого мы воспользуемся матрицей. Матрица - упорядоченный в строки и столбцы набор чисел. Векторы умножаются на матрицы по определённым правилам, изменяя значения вектора заданным способом.

В GLSL есть встроенная поддержка двух- трёх- и четырёхмерных матриц: mat2 (2x2), mat3 (3x3) и mat4 (4x4). GLSL так же поддерживает умножение матриц (*) и некоторые специальные функции (matrixCompMult()).

Мы можем конструировать матрицы, приводящие к определённому поведению. Например, можно использовать матрицу для переноса вектора:

Что более интересно, мы можем использовать матрицу для поворота системы координат:

Взгляните на код функции, которая конструирует двумерную матрицу поворота. Эта функция повторяет приведённую выше формулу для вращения вектора вокруг точки vec2(0.0).

mat2 rotate2d(float _angle){
    return mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle));
}

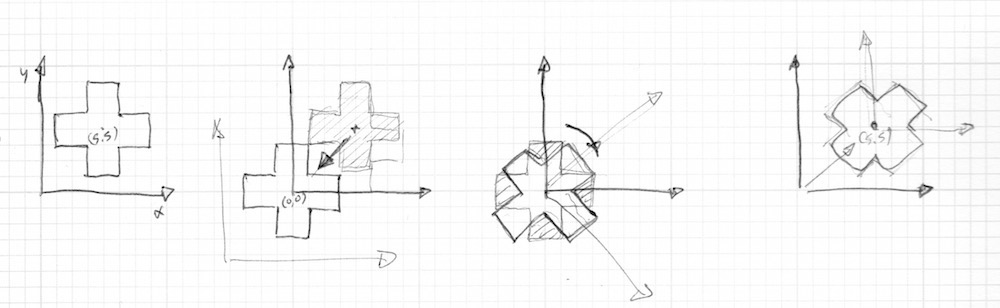
Это не совсем то что нам нужно, если мы вспомним наш способ пострения геометрических фигур. Фигура креста нарисована в центре изображения, то есть в точке vec2(0.5). Поэтому, прежде чем поворачивать пространство, нам нужно передвинуть фигуру из центра в точку vec2(0.0), и только после этого повернуть пространство, и в конце не забыть передвинуть фигуру в исходное положение.

Рассмотрите код:

Попробуйте выполнить следующее:

• Раскомментируйте строку 45 и посмотрите что происходит.

• Закомментируйте сдвиги до и после поворота в строках 37 и 39, понаблюдайте за последствиями.

• Используйте вращение, чтобы улучшить анимацию, которую вы сделали в упражнении про перенос.

Масштаб

Мы увидели как можно использовать матрицы для переноса и поворота объектов в пространстве. Или, точнее, как трансформировать систему координат для вращения и движения объектов. Если вы пользовались софтом для 3D-моделирования или функциями push и pop для матриц в Processing, вы скорее всего знаете, что с помощью матриц можно ещё и масштабировать объекты.

Следуя этой формуле, можно понять как делается двумерная матрица масштабирования.

mat2 scale(vec2 _scale){
    return mat2(_scale.x,0.0,
                0.0,_scale.y);
}

Выполните следующие упражнения для более глубокого понимания того, как это работает.

• Раскомментируйте строку 42 в коде выше и пронаблюдайте масштабирование пространственных координат.

• Посмотрите что произойдёт, если закомментировать переносы в строках 37 и 39.

• Попробуйте скомбинировать матрицы масштабирования и поворота. Помните, что порядок важен. Сначала перемножьте матрицы, а затем умножайте результат на векторы.

• Теперь когда вы умеете рисовать различные фигуры и управлять их положением в пространстве, мы можем приступить к композиции. придумайте и нарисуйте бутафорский интерфейс пользователя или HUD (heads up display, то есть когда информация проецируется на стекло шлема или транспортного средства). Для поиска идей используйте следующий пример с ShaderToy, написанный пользователем Ndel.

Другие применения матриц: цвет в пространстве YUV

YUV - цветовое пространство для аналогового кодирования фото и видео, разработанное с учётом особенностей восприятия человека чтобы снизить требования к каналу передачи компонентов цвета.

В следующем коде матричные операции GLSL используются весьма интересно - с их помощью сделано преобразование из одного цветового пространства в другое.

Здесь мы трактуем цвета как векторы и умножаем их на матрицы. Таким образом, мы "перемещаем" значения цвета.

В этой главе мы научились использовать матричные преобразования для сдвига, поворота и масштабирования векторов. Эти трансформации очень важны при построении композиций из фигур, которые мы рисовали в предыдущей главе. А в следующей главе мы используем все полученные знания для создания красивых процедурных узоров. Вы увидите, что программирование повторений и изменений может быть захватывающим занятием.