## Matrizes 2D
### Translação
No capítulo anterior, aprendemos como fazer algumas formas básicas - o macete para mover essas formas é mover o próprio sistema de coordenadas. Podemos fazer isso simplesmente adicionando um vetor à variável ```st``` que contém a localização de cada fragmento. Isso faz com que todo o sistema de coordenadas espaciais se mova.
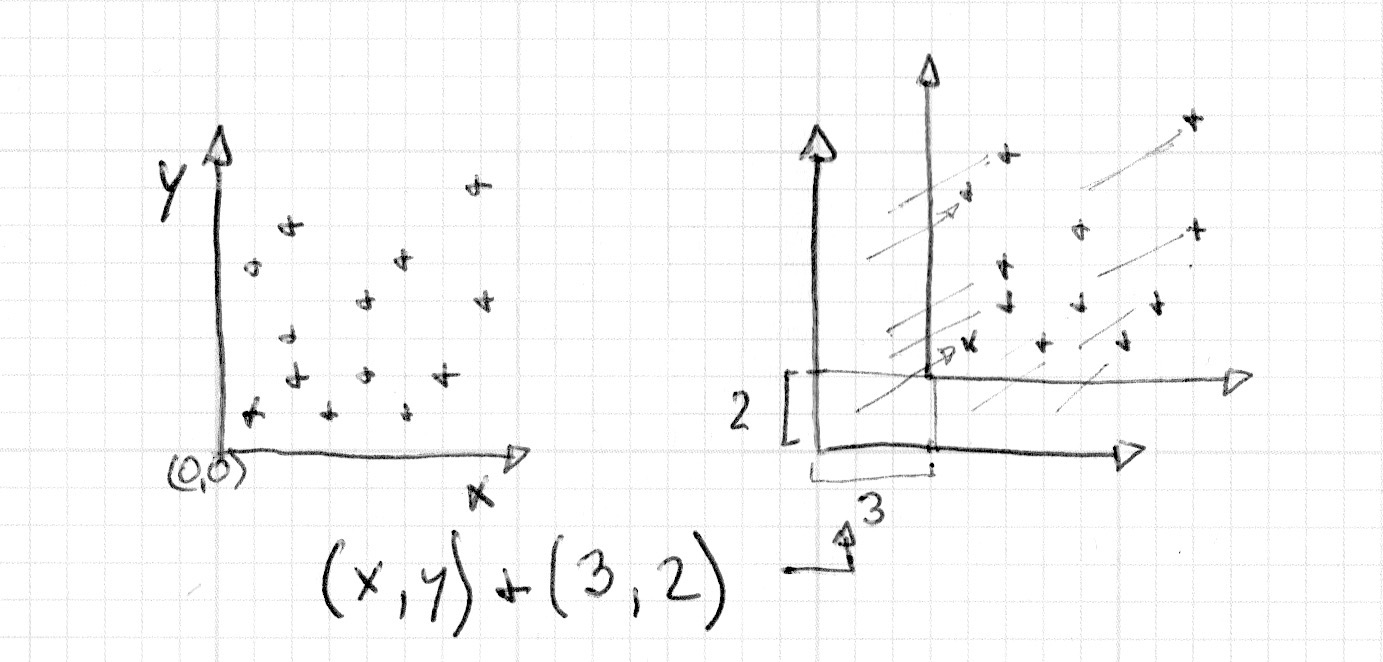
Isso é mais fácil de ver do que explicar, então, veja por você mesmo:
* Descomente a linha 35 do código acima para ver como o espaço se move.
Agora, tente o seguinte exercício:
* Usar ```u_time``` junto com funções de forma, mova a pequena cruz de uma forma interessante. Procure por uma qualidade específica de movimento que você esteja interessado e tente fazer a cruz se mover do mesmo jeito. Gravar algo do "mundo real" primeiro pode ser útil - poderia ser o ir e vir das ondas, um movimento de um pêndulo, uma bola saltitante, um carro acelerando, uma bicicleta parando.
### Rotações
Para rotacionar objetos, também precisamos mover o sistema espacial inteiro. Para isso, vamos usar uma [matriz](http://en.wikipedia.org/wiki/Matrix_%28mathematics%29). Uma matriz é um conjunto organizado de números em colunas e linhas. Vetores são multiplicados por matrizes seguindo um conjunto preciso de regras de forma a modificar os valores do vetor de maneira particular.
[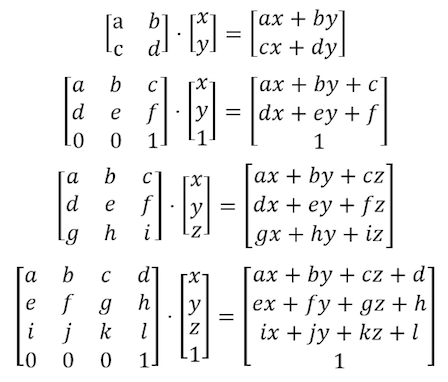](https://en.wikipedia.org/wiki/Matrix)
GLSL tem suporte nativo para matrizes de duas, três e quatro dimensões: [```mat2```](../glossary/?search=mat2) (2x2), [```mat3```](../glossary/?search=mat3) (3x3) and [```mat4```](../glossary/?search=mat4) (4x4). GLSL também suporta multiplicação de matrizes (```*```) e uma função específica de matrizes ([```matrixCompMult()```](../glossary/?search=matrixCompMult)).
Baseado em como as matrizes se comportam, é possível construir matrizes para produzir comportamentos específicos. Por exemplo, podemos usar uma matriz para transladar um vetor:
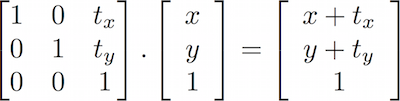
Mais interessante ainda: podemos usar uma matriz para rotacionar o sistema de coordenadas:
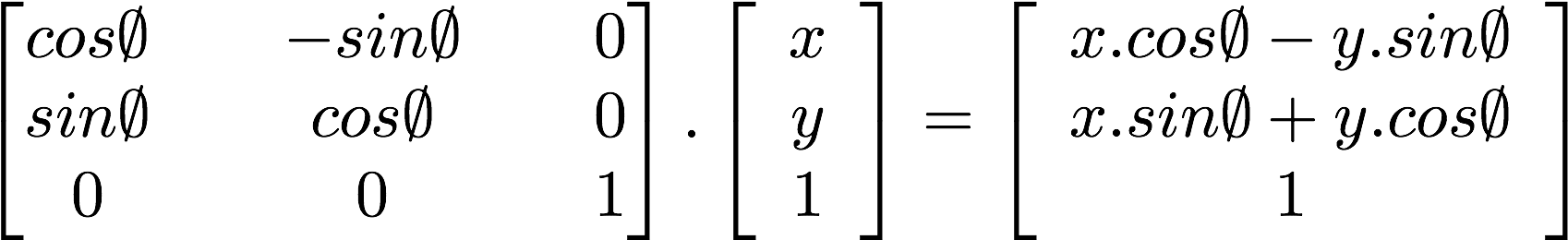
Dê uma olhada no código a seguir para ver uma função que constrói uma matriz de rotação 2D. Essa função segue a [fórmula](http://en.wikipedia.org/wiki/Rotation_matrix) acima para vetores de duas dimensões, para rotacionar as coordenadas em torno do ponto ```vec2(0.0)```.
```glsl
mat2 rotate2d(float _angle){
return mat2(cos(_angle),-sin(_angle),
sin(_angle),cos(_angle));
}
```
De acordo com a forma como estamos desanhando nossas formas, não é isso, exatamente, o que queremos. Nossa forma de cruz é desenhada no meio da tela, o que corresponde à posição ```vec2(0.5)```. Então, antes de rodarmos o espaço, precisamos mover a forma do `center` para a coordenada ```vec2(0.0)```, rotacionar o espaço, e finalmente mover de volta para o lugar original.
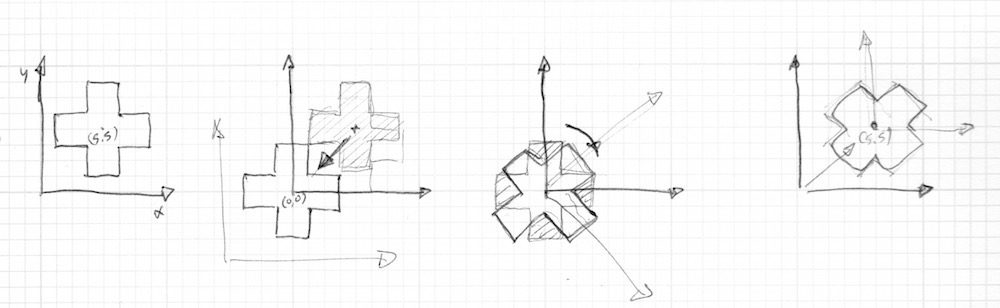
Isso se parece com o seguinte código:
Tente os exersícios a seguir:
* Descomente a linha 45 do código acima, e preste atenção no que acontece.
* Comente as translações antes e depois da rotação, nas linhas 37 e 39, e observe as consequências.
* Use rotações para melhorar a animação que você simulou no exercício de translação.
### Escala (scale)
Vimos como as matrizes são usadas para transladar e rotacionar objetos no espaço (ou, mais precisamente, transformar o sistema de coordenadas para rotacionar e mover objetos). Se você já usou softwares de modelagem 3D ou as funções de push e pop no Processing, já sabe que as matrizes também podem ser usadas para escalar o tamanho de um objeto.

Seguindo a fórmula anterior, você pode calcular como fazer uma matriz para escalar em 2D:
```glsl
mat2 scale(vec2 _scale){
return mat2(_scale.x,0.0,
0.0,_scale.y);
}
```
Tente os seguintes exersícios para entender mais a fundo como isso funciona.
* Descomente a linha 42 do código acima, para ver a coordenada de espaço sendo escalada.
* Veja o que acontece quando você comenta as translações antes e depois de escalar, nas linhas 37 e 39.
* Tente combinar uma matriz de rotação com uma de escala. Tenha em mente que a ordem faz diferença. Multiplique pela matriz primeiro e então multiplique os vetores.
* Agora que você sabe como desenhar formas diferentes, e mover, rotacionar e escalá-las, é hora de fazer uma composição bem maneira. Projete e construa um [HUD (heads up display) ou UI falso](https://www.pinterest.com/patriciogonzv/huds/). Use o seguinte ShaderToy de exemplo, do [Ndel](https://www.shadertoy.com/user/ndel) como inspiração e referência.
### Outros usos para matrizes: cores YUV
[YUV](http://en.wikipedia.org/wiki/YUV) é um espaço de cores usado para codificação analógica de fotos e vídeos, que considera o faixa da percepção humana para reduzir a largura de banda dos componentes de crominância.
O código a seguir é uma oportunidade interessante para usar operações de matrizes em GLSL para transformar as cores de um modo para outro.
Como você pode ver, estamos tratando as cores como vetores, multiplicando-os com matrizes. Dessa forma, nós "movemos" os valores.
Neste capítulo, aprendemos como usar transformações de matrizes para mover, rotacionar e escalar vetores. Essas transformações serão essenciais para fazer composições com as formas que aprendemos no capítulo anterior. No próximo capítulo, vamos aplicar tudo o que aprendemos para fazer padrões procedurais bem bonitos. Você vai achar que a repetição e variação na programação podem ser uma prática excitante.