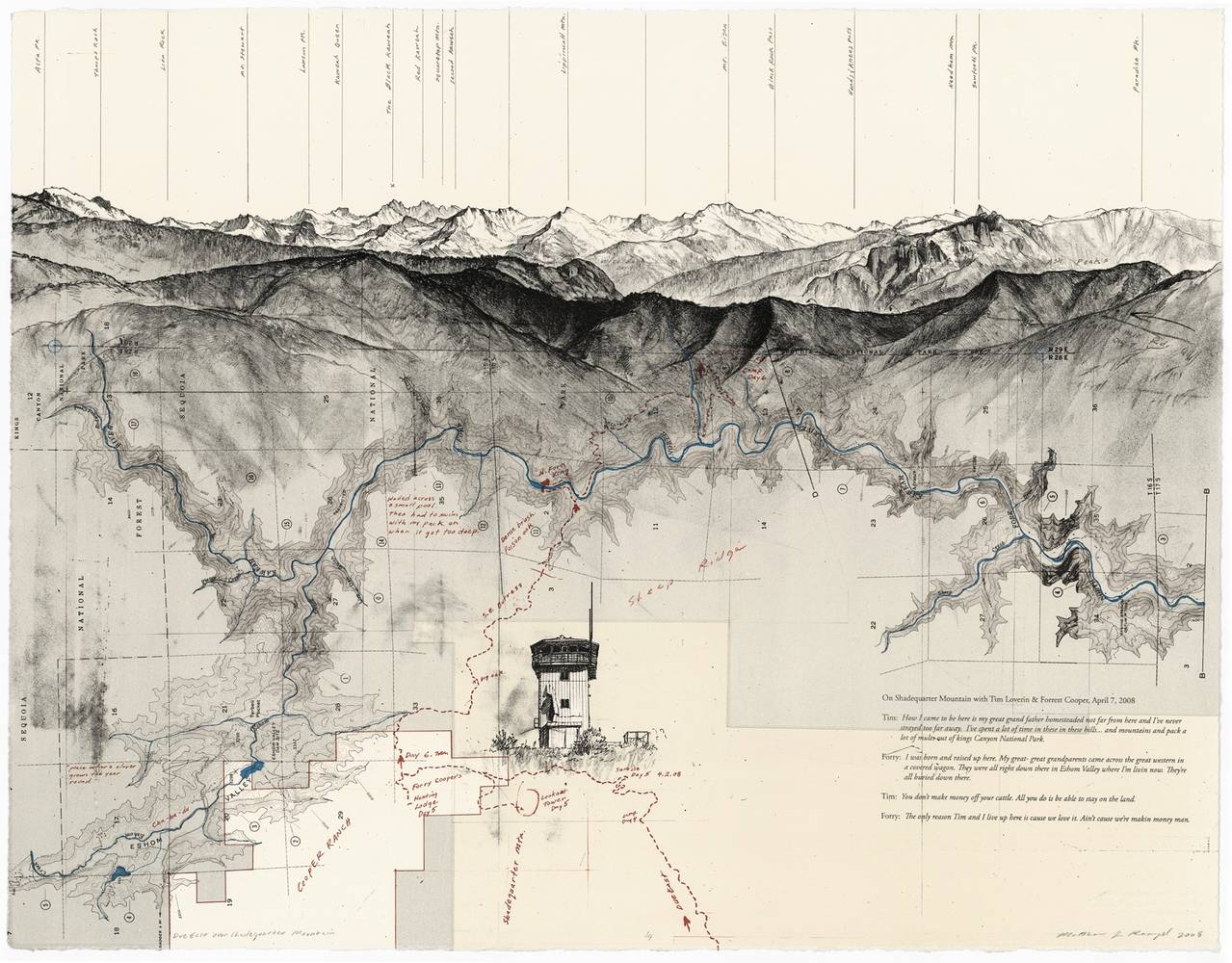
## Fractional Brownian Motion
Le bruit peut avoir plusieurs significations selon les personnes. Les musiciens le trouveront dérangeant, les communicants le considèrent comme une interférence et les astrophysiciens comme un rayonnement cosmique.
Toutes ces qualifications, nous ramènent à l'ancrage *physique* du bruit dans notre environnement. Commençons toutefois par quelque chose de plus simple et de plus fondamental ; les ondes et leurs propriétés.
Une onde peut être considérée comme la variation d'une propriété dans le temps ; le son est une variation de la pression de l'air au fil du temps, une onde électro-magnétique est la fluctuation dans le temps d'un champs électrique et magnétique etc.
Les deux caractéristiques importantes d'une onde sont sa *fréquence* et son *amplitude*.
L'équation d'une onde à une dimension peut s'écrire comme suit:
* Essayez de changer les valeurs de fréquence et d'amplitude pour comprendre leurs effets.
* À l'aide des fonctions de formes, faites varier l'amplitude au fil du temps.
* Faites de même avec la fréquence.
Félicitations! en suivant les deux dernières instructions, vous avez réussi à "moduler" l'onde et à créer une modulation de fréquence (FM) et d'amplitude (AM), et oui, exactement comme des ondes radio!
Une seconde propriété intéressante des ondes est leur capacité à s'additionner, ce qu'on appelle la superposition.
Commentez/décommentez et jouez avec les les lignes suivantes en vous intéressant à la forme que prend l'onde lorsqu'on la combine à d'autres.
* Changez les valeurs de fréquence et d'amplitude des ondes additionnelles.
* Pouvez vous créer deux ondes qui s'annulent? à quoi ressemblera l'onde finale?
* Est-il possible d'additionner des ondes de manière à ce qu'elles s'amplifient l'une l'autre?
En musique, chaque note est associée à une fréquence particulière. Les fréquences correspondent aux _notes_ de musique et doubler ou diviser par deux une fréquence permet de changer d'_octave_.
Utilisons à présent un bruit de Perlin au lieu d'une sinusoïde!
Un bruit de Perlin de base ressemble globalement à une sinusoïde.
Son amplitude et sa fréquence varient un peu mais l'amplitude reste globalement la même tandis que la fréquence
reste cantonnée dans une zone restreinte autour de la fréquence centrale.
Cependant, ce n'est pas une sinusoïde régulière et il est plus simple d'atteindre un résultat pseudo-aléatoire
en ajoutatnt plusieurs versions du bruit à différentes échelles (amplitudes).
Il est possible d'obtenir le même résultat avec des sinusoïdes mais il est nécessaire de combiner un nombre d'ondes important pour masquer leur nature périodique.
En ajoutant différentes itérations du **bruit** (différents *octaves*),
dont on augmente la fréquence (la *lacunarité*) et dont on réduit l'amplitude (le *gain*), on obtient une granularité
qui nous permet de préserver les détails fins d'un bruit.
Cette technique s'appelle "Fractional Brownian Motion" (*FBM*) ou simplement *bruit fractal*
Voici un exemple d'implémentation:
* Changez progressivement le nombre d'octaves de 1 à 10 et regardez ce qui se produit.
* Au delà de 4 octaves, changez la valeur de lacunarité.
* toujours au delà de 4 octaves, changez le gain et observez le résultat.
Notez comment, à chaque nouvel octave, la courbe semble gagner en détail.
Notez également lors de l'ajout d'octaves que lorsqu'on zoome sur la courbe, les plus petits éléments ressemblent à l'ensemble et inversement ; c'est ce qu'on appelle l'*auto-similarité*:
C'est une propriété importante des fractales et nous la simulons dans notre boucle.
Nous ne créons pas une fractale à proprement parler puisque nous arrêtons l'ajout de bruit après quelques itérations mais d'un point de vue théorique,
si nous pouvions laisser la boucle tourner indéfiniment et ajouter une somme infinies de bruits, nous obtiendrions une courbe fractale.
Dans un shader, la finesse du détail est limitée par la résolution écran ; si le résultat devient plus petit qu'un pixel, il n'ya pas vraiment de raison (ni de moyen) de le représenter à l'écran.
Nous avons donc pas besoin de boucles infinies pour obtenir une apparence fractale, il faut parfois un grand nombre d'itérations mais jamais une inifinité.
le code suivant est un exemple d'implémentation de **FBM** en 2 dimensions:
* Réduisez le nombre d'octaves en changeant la ligne 37
* Changez la lacunarité du FBM à la ligne 47
* Changez le gain ligne 48
Cette technique est communément utilisée pour créer des terrains procéduraux.
l'*auto-similarité* du FBM se prête bien au rendu de montagnes ; le processus d'érosion qui donne leur forme aux montagnes
produit le même genre de motifs auto-similaires à grande échelle.
Si le sujet vous intéresse, nous vous invitons à lire [cet article d'Inigo Quiles sur les techniques de bruit avancées](http://www.iquilezles.org/www/articles/morenoise/morenoise.htm).
Le principe du **FBM** peut être amendé pour obtenir différents effets comme par exemple cette **turbulence**.
On part de la structure de notre FBM mais au lieu d'accumuler la valeur signée(+/-) du bruit, on accumule sa valeur absolue(+) ce qui crée des *vallées* et des *collines*.
```glsl
for (int i = 0; i < OCTAVES; i++) {
value += amplitude * abs(snoise(st));
st *= 2.;
amplitude *= .5;
}
```
Une seconde variante dite *ridge noise* (bruit de *crête* ou d'*arête*) consiste à inverser les vallées:
```glsl
n = abs(n); // create creases
n = offset - n; // invert so creases are at top
n = n * n; // sharpen creases
```
Une autre variante consiste à multiplier les valeurs de bruit au lieu de les additionner.
Il est intéressant de modifier l'échelle d'une itération de bruit en fonction du bruit de l'itération precédente.
En faisant ce genre de chose, nous nous éloignons du monde des fractales et entrons dans le monde méconnu des *multifractales*.
Les *multifractales* ne sont pas aussi clairement définies mathématiquement que les fractales ce qui ne nous empêche pas de nous en servir dans les shaders.
Les simulations *multifractales* sont d'ailleurs très répandues dans les logiciels de génération de terrain.
Vous trouverez plus d'informations sur ce sujet au chapitre 16 de "Texturing and Modeling: a Procedural Approach" (3ème édition), de Kenton Musgrave.
Malheureusement le livre n'est plus édité depuis quelques années déjà mais vous le trouverez en bibliothèque ou d'occasion.
Il est possible d'acheter un PDF de la première édition en ligne mais ça ne vaut pas le coup ; elle date de 1994 et ne contient aucune information sur la génération de terrain.
### Domain Warping
[Inigo Quiles a également écrit cet article fascinant](http://www.iquilezles.org/www/articles/warp/warp.htm) sur le fait de "plier" ou "recouvrir" (*wrap*) l'espace d'un FBM à l'aide d'un FBM.
ce serait le *rêve dans le rêve* d'Inception.
Le code suivant est une variation moins spectaculaire de cette technique, on utilise le *wrapping* (pliage, recouvrement, emballage) pour créer une sorte de nuage.
Notez la part que joue l'*auto-similarité* dans le résultat final.
Le fait de *wrapper* (plier, recouvrir, emballer) ainsi les coordonnées de textures peut être extrêmement utile, relativement amusant et terriblement dur à maîtriser.
C'est un outil puissant qui demande beaucoup de pratique pour être correctement utilisé.
["Flow noise", un célèbre article de Ken Perlin et Fabrice Neyret](http://evasion.imag.fr/Publications/2001/PN01/) explique comment utiliser les dérivées (ou dégradés) du bruit pour atteindre ce résultat.
Les implémentations récentes du bruit de Perlin se servent à la fois de la fonction et de sa dérivée.
Si la *vraie* dérivée n'est pas disponible, on peut toujours se rabattre sur les différences finies pour l'approcher bien que ce soit moins précis et demande plus de travail.